Автор: Андрей Винокуров

В настоящей статье вы найдете описание традиционной архитектуры построения блочных шифров, лежащей в основе наиболее известных из современных несекретных шифров, таких, как Российский и американский стандарты шифрования. Статья была написана ровно 3 года назад – автор закончил ее в первой половине апреля 1995 года, но по разным причинам не смог тогда опубликовать. В то время информация по архитектуре классических блочных шифров практически отсутствовала в Российской открытой печати, а русскоязычная терминология в этой области находилась еще в стадии становления. За прошедшее с тех пор время появилось огромное число материалов по обсуждаемой теме, поэтому сегодня статья может показаться слегка наивной. Однако ее коренная переделка заняла бы слишком много времени, проще написать новую статью, и поэтому автор параллельно с этой работой решил опубликовать текущую версию с незначительными изменениями. Статья не предполагает предварительного знакомства читателя с криптографией, однако содержит достаточное числ

о математических формул и подразумевает владение соответствующим математическим аппаратом.

Введение

Заканчивающееся 20-е столетие является веком не только электричества и атома, в еще большей степени оно может претендовать на то, чтобы называться веком тотальной информатизации и компьютеризации общества. С того самого момента, когда в его середине появились и начали победное шествие по планете устройства для обработки цифровых данных – компьютеры, возникла индустрия производства, обработки и потребления информации, которая в настоящее время стала неотъемлемой частью нашей жизни. Сейчас о технологическом уровне государств имеет смысл судить не по количеству выплавляемой на душу населения стали или производимых комбайнов для уборки сахарной свеклы, а по совокупной мощностью всех вычислительных средств, приходящихся на одного жителя страны.

О важности информации в современном мире наиболее показательно свидетельствуют следующие факты: Во-первых, обладание определенным цифровым кодом может открыть доступ его владельцу к значительным материальным ценностям и услугам – такое положение вещей имеет место благодаря тому, что информатизация общества не обошла стороной банковско-финансовую сферу. Во-вторых, сложилась и необычайно окрепла индустрия информационных услуг – информация стала обыкновенным товаром, то есть объектом купли–продажи. Многие фирмы преуспевают только благодаря тому, что могут получить важные для их деятельности сведения всего на несколько часов или суток раньше своих конкурентов. В третьих, по оценкам зарубежных экономистов значительная доля западных фирм разорилась бы в течении нескольких дней после разглашения критически важной информации, лежащей в основе их деятельности.

Особый, нематериальный характер информации делает исключительно легким ее копирование и модифицирование, в силу чего она становится соблазнительным объектом различного рода злоупотреблений. Кроме того, довольно типичной является ситуация, когда нужную кому-либо информацию ее владельцы не согласились бы продать ни за какие деньги, и единственный способ ее получить – это украсть. Указанные причины привели к возникновению целой отрасли человеческой деятельности, основное назначение которой – добывать информацию любыми возможными и невозможными способами, – конечно же, речь идет о разведке. Профессия шпиона наряду с другими, прекрасно всем известными, является одной из древнейших на планете. С другой стороны, статистика неумолимо свидетельствует, что все большая доля всех преступлений совершается в сфере информационных технологий “белыми” и “синими воротничками”, использующими “бреши” информационных систем в своих личных целях. Действительно, сейчас, чтобы ограбить банк, не нужно проламывать стены хранилищ и резать автогеном сейфы, достаточно узнать код, управляющий доступом к одному из банковских счетов. Все, что для этого требуется, – это компьютер и доступ к банковской сети, ну и конечно, некоторое количество серого вещества в черепной коробке. Прискорбно, но факт – число преступлений с использованием “высоких технологий” растет быстрыми темпами.

Высокая уязвимость информационных технологий к различным злоумышленным действиям породила острую необходимость в средствах противодействия этому, что привело к возникновению и развитию области защиты информации (ЗИ) как неотъемлемой части информационной индустрии. Древнейшей задачей сферы ЗИ является защита передаваемых сообщений от несанкционированного ознакомления с их содержимым, имеются свидетельства понимания людьми этой проблемы еще в до-античные времена – в древнем Египте и Вавилоне, а информация о способах ее решения в античном мире дошла до нас в виде ссылок на так называемый “код Цезаря” – простейший шифр, применяемый сначала Юлием Цезарем, а впоследствии и другими Римскими императорами, для защиты своей переписки от излишне любопытных глаз. Однако вплоть до нового времени тайнопись была не ремеслом, а искусством, и как наука, криптография сложилась лишь в настоящем веке. Но еще долгое время после этого шифровальные отделы были исключительной прерогативой дипломатических и разведывательных служб,

ситуация кардинально изменилась только в последние десятилетия.

В настоящее время понятие “защита информации” объединяет в себе множество самых различных значений – от резервирования питания для защиты информации от разрушения при возможных сбоях в питающей сети и охранников в дверях компьютерного зала, препятствующих входу посторонних лиц и выносу сотрудниками носителей информации, до генераторов помех, “глушащих” уносящие информацию излучения. Из всего многообразия методов ЗИ нас с вами интересуют лишь те, которые никак не связаны с характеристиками ее материальных носителей, а основаны на манипулировании самой информацией и используют лишь ее имманентные свойства. Эта область ЗИ именуется криптографической защитой информации и переживает сейчас настоящий бум. На сегодняшний день известно большое количество задач, относящихся к сфере ЗИ, – такое обилие обусловлено тем, что информационные взаимодействия, развиваясь, приобретают все более сложный характер, соответственно становятся более разнообразными и изощренными угрозы в их сторону, а это в свою очередь приводит к возникновению новых задач. Если раньше все потребности в защите информации сводились к обеспечению секретности и подлинности передаваемых сообщений, то есть к их защите от чтения и внесения изменений посторонними лицами, то сейчас актуально гораздо большее число проблем. Среди новых задач отметим лишь две, наиболее известные: рассылка секретных ключей по незащищенным каналам связи (открытое распределение ключей) и подтверждение авторства сообщений (цифровая подпись). А ведь существует большое количество менее известных, но не менее важных задач.

Соответственно классам решаемых задач в настоящее время сложились две области криптографии: классическая, или криптография с секретным ключом, и современная, или криптография с открытым ключом. История первой насчитывает тысячелетия, тогда как официальный возраст второй не перевалил еще за три десятка лет. Кратко остановимся на различиях между ними.

1. Классическая и современная криптография.

Классическая, или одно-ключевая криптография решает фактически лишь две задачи: защиту передаваемых сообщений от прочтения и от модификации посторонними лицами. Она опирается на использование симметричных алгоритмов шифрования, в которых за- и расшифрование отличаются только порядком выполнения и направлением некоторых простых шагов. Эти алгоритмы используют один и тот же секретный элемент (ключ), и второе действие (расшифрование) является простым обращением первого (зашифрования). Поэтому каждый из участников обмена может как зашифровать, так и расшифровать сообщение. По причине большой избыточности естественных языков непосредственно в зашифрованное сообщение чрезвычайно трудно внести осмысленное изменение, поэтому классическая криптография обеспечивает также защиту от навязывания ложных данных. Если же естественной избыточности оказывается недостаточно для надежной защиты сообщения от модификации, она может быть искусственно увеличена путем добавления к нему специальной контрольной комбинации, называемой имитовставкой.

Классическая схема шифрования прекрасно работает, пока между участниками информационного обмена есть взаимное доверие. Если же его нет, то могут возникать различные коллизии, так как из-за полной симметрии схемы в случае конфликта между сторонами для независимого наблюдателя нет возможности сделать однозначный вывод, кто из двух участников прав. Действительно, получатель может сам изготовить зашифрованное сообщение и затем объявить, что оно им получено от законного отправителя, а тот, в свою очередь, может отказаться от авторства в действительности переданного им сообщения, объявив, что его сфабриковал сам получатель, благо соответствующая возможность у того имеется. В этих случаях независимый арбитраж, в функции которого входит разрешение конфликтов между участниками информационного процесса, не сможет определить, кто из них прав, а кто – нет. Приведенный факт означает, что рассматриваемая криптографическая схема не позволяет однозначно подтвердить или опровергнуть авторство сообщения. Кроме того, эта схема нуждается в специальной службе, занимающейся изготовлением секретных ключей и доставкой их участникам информационного обмена. Конечно, если участников обмена всего двое, то проблема невелика – роль такой службы может выполнять один из них или даже оба они попеременно. Но если система насчитывает сотни или даже тысячи связанных между собой узлов обработки информации, это небольшая проблема вырастает в большую головную боль.

Противоречие между ограничениями классической криптографии и постоянно возникающими новыми задачами привело к тому, что во второй половине семидесятых годов были разработаны принципиально новые подходы, позволяющие решить как перечисленные выше проблемы, так и большое число других. Основой послужило открытие так называемых асимметричных криптоалгоритмов, или методов, в которых процедуры прямого и обратного криптопреобразования выполняются на различных ключах и не имеют между собой очевидных и легко прослеживаемых связей, которые позволили бы по одному ключу определить другой. В такой схеме знание только ключа зашифрования не позволяет расшифровать сообщение, поэтому он не является секретным элементом шифра и обычно публикуется участником обмена для того, чтобы любой желающий мог послать ему шифрованное сообщение.

Как видим, современная криптография позволяет решить гораздо более широкий круг задач, чем криптография классическая. На заре ее развития высказывались даже мнения, что она за несколько лет полностью вытеснит свою предшественницу, однако этого не произошло по следующим причинам: Во-первых, алгоритмы с секретным ключом гораздо проще реализуются как программно, так и аппаратно, в силу чего при одинаковых характеристиках производительности и стойкости сложность, а значит и цена аппаратных средств, реализующих шифр с открытым ключом заметно выше цены аппаратуры, реализующей классический шифр, а при программной реализации на одном и том же типе процессора одноключевые шифры работают быстрее двухключевых. Во-вторых, надежность алгоритмов с открытым ключом в настоящее время обоснована гораздо хуже, чем надежность алгоритмов с секретным ключом и нет гарантии, что через некоторое время они не будут раскрыты, как это получилось с криптосистемой, основанной на задаче об укладке ранца. Поэтому для организации шифрованной связи в настоящее время применяются исключительно классические шифры, а методы современной криптографии используются только там, где они не работают, то есть для организации различных хитроумных протоколов типа цифровой подписи, открытого распределения ключей и игры в покер по переписке. Поскольку асимметричные криптографические алгоритмы не являются темой настоящей статьи, автор не будет более задерживаться на этом. Заинтересованный читатель может найти их описание и обсуждение в большом количестве источников, например, в [1,3,4,8].

Необходимо отметить, что в настоящее время публикуется значительное число научных и популярных работ по современной криптографии, тогда как немногочисленные публикации, в которых рассматриваются классические шифры, посвящены в основном или вопросам истории искусства тайнописи, или содержат описание конкретных алгоритмов без исследования общих принципов, лежащих в их основе. Такое положение вещей с одной стороны, является данью моде, а с другой – последствием чрезмерной засекреченности классической криптографии, во всяком случае, нормальным его назвать нельзя. Именно поэтому в настоящей работе автор решил рассказать об общих принципах построения криптоалгоритмов с секретным ключом, точнее, одного из его классов, называемых блочными шифрами, на достаточно простом уровне, чтобы статья была понятна даже не очень подготовленному читателю, и вместе с тем с необходимой строгостью. Нет необходимости подробно расписывать достоинства рассматриваемых в статье принципов построения алгоритмов шифрования, достаточно лишь сказать, что они лежат в основе двух наиболее известных в России шифров из числа самых сильных, или, если вам так больше нравится, двух наиболее сильных шифров из числа самых известных – Российского и американского стандартов шифрования, алгоритмов ГОСТ 28147-89 и DES, а также большого числа менее известных и/или менее сильных шифров. Перейдем непосредственно к их изучению.

2. Основные понятия.

Существует несколько принципов построения криптоалгоритмов с секретным ключом – различают потоковые и блочные шифры, можно провести классификацию и по другим признакам. Чтобы рассказать о всех возможных типах шифров данного класса необходимо написать не статью, а довольно объемистую книгу или даже несколько книг. Поэтому автор не будет пытаться объять необъятное, и ограничится в данной статье рассказом об архитектуре, воплощенной в Российском и американском стандартах шифрования – при всех их различиях они похожи как братья, пусть даже и не близнецы. Быть может, изложенные в статье сведения вдохновят читателя с пытливым умом на создание собственного шифра – в этом нет ничего невозможного, ведь криптография в последние годы достигла таких успехов, что сейчас даже наименее развитые в науке страны, не говоря уже о крупных процветающих фирмах из развитых государств, могут позволить себе создать практически нераскрываемый шифр. Тому есть яркий пример – американский стандарт шифрования (DES) первоначально был ра зработан фирмой IBM для своих собственных нужд, и лишь затем, после некоторых переработок, был принят в качестве федерального стандарта США [2]. Достижения современной криптографии позволяют обеспечить настолько полную конфиденциальность при обработки информации, что даже самые ярые поборники приватности и невмешательства государства в личные дела граждан опасаются ее последствий. Так, Конгрессом Соединенных Штатов рассматриваются законодательные акты, разрешающие применение криптографических средств только под контролем соответствующих служб. При этом все процедуры обмена шифрованными сообщениями должны строиться таким образом, что бы при необходимости спецслужбы по решению судебных органов могли их дешифровать. Возможно, что достаточно скоро до этого дойдет дело и у нас. В этом направлении уже сделано несколько шагов – прочитайте указ президента России №334 от 3 апреля 1995 года “О мерах по соблюдению законности в области разработки, производства, реализации и эксплуатации шифровальных средств, а также

предоставления услуг в области шифрования информации”, фактически устанавливающий государственный контроль за разработкой и использованием средств криптозащиты информации. Сомнений насчет того, откуда “уши растут” быть не может – ФАПСИ намерено быть монополистом на этом весьма привлекательном рынке аппаратов, программ и услуг, а государство не хочет, чтобы его граждане имели секреты от него.

Вернемся к сути проблемы: итак, пусть две стороны, которые мы назовем законными участниками обмена информацией, пытаются наладить секретную связь. Из них один является отправителем, а другой – получателем сообщения, хотя, конечно, в реальных ситуациях эти роли не закреплены за участниками жестко и каждому из них приходится быть как отправителем, так и получателем. Задача отправителя заключается в том, чтобы сформировать и отправить получателю сообщение T. Задача получателя заключается в том, чтобы посланное сообщение получить и понять его содержание. Чтобы один только получатель мог ознакомиться с содержанием сообщения, отправителю необходимо преобразовать его согласно некоторому алгоритму E таким образом, что бы ни кто, за исключением законного получателя и, быть может, самого отправителя, не мог восстановить его в прежнем виде. Это преобразование называется зашифрованием сообщения T, а то, что получается в результате этой процедуры, называется шифротекстом T'. Связь между исходным текстом T, шифротекстом T' и алгоритмом зашифрования E может быть символически выражена с помощью следующей формулы: T' = E(T). Шифрованное сообщение T' передается отправителем получателю по каналу связи. Чтобы законный получатель мог ознакомиться с содержимым полученного сообщения, он должен предварительно его расшифровать, то есть применить к шифротексту T' алгоритм расшифрования D, в результате чего будет восстановлено исходное сообщение T. Таким образом, расшифрование данных осуществляется согласно уравнению T = D(T'). Чтобы обеспечить секретность связи, алгоритм расшифрования не должен быть известен посторонним лицам, так как его секретность определяет секретность организованной таким образом связи.

В нашей ситуации присутствует третья сторона, называемая согласно сложившейся традиции злоумышленником, которая желает воспрепятствовать осуществлению намерений законных участников обмена. В наиболее общем случае во исполнение своих намерений злоумышленник может перехватывать шифрованные сообщения и посылать сфабрикованные им самим сообщения одной из сторон от имени другой. Конечно, он не владеет алгоритмом расшифрования – в этом случае все было бы предельно просто для него. Круг задач, которые может попытаться решить криптоаналитик, шире чем просто дешифрование сообщения – перечислим эти задачи, именуемые в криптографии угрозами:

• дешифровать сообщение T', то есть получить соответствующий ему открытый текст T' полностью или частично, или хотя бы сделать некоторые заключения о содержании перехваченного сообщения, опираясь на обнаруженные в нем закономерности;
• сформировать на основе имеющихся у него данных сообщение T~', которое законный получатель принял бы за подлинное. При этом вовсе не обязательно, хотя, конечно, весьма желательно для злоумышленника, чтобы он сам мог понимать смысл составленного сообщения или даже мог сфабриковать любое выбранное им по своему усмотрению сообщение;

Под раскрытием шифра понимают успешную реализацию хотя бы одной из указанных угроз. Первая угроза, если будет осуществлена, нарушит секретность сообщения, а вторая нарушит его подлинность. Степень успеха в реализации перечисленных выше угроз также может быть различной. Если исключить случайную удачу, то успешная реализация угрозы секретности данных означает овладение злоумышленником алгоритмом расшифрования D, или построение функционально эквивалентного ему алгоритма D', позволяющего для любого зашифрованного сообщения T', или хотя бы для шифротекстов из некоторого класса, получить соответствующее открытое сообщение T. Аналогично, успешная реализация угрозы целостности данных означает овладение злоумышленником алгоритмом зашифрования E, или построение функционально эквивалентного ему алгоритма E', позволяющего для любого открытого сообщения T, или хотя бы для сообщений из некоторого класса, получить соответствующее зашифрованное сообщение T', или, в наименее успешном для него случае, создание алгоритма E~

позволяющего создать такое зашифрованное сообщение T', которое законный получатель принял бы за подлинное.

Для осуществления своих угроз злоумышленнику требуется выполнить некоторую достаточно интеллектуальную работу с перехваченными данными, в этом ему может помочь криптоаналитик. Нетрудно догадаться, что в задачу последнего входит криптоанализ, то есть анализ перехваченных сообщений с целью осуществления одной из перечисленных выше угроз. При этом аналитик может располагать следующей информацией:

• дешифруемый текст T', также могут иметься перехваченные ранее шифрованные сообщения
  (T1' ,T2',...,Tn' ), зашифрованные с использованием того же самого алгоритма, что и T';
• открытые сообщения, соответствующие некоторым ранее перехваченным шифровкам:
  (T1,T2,...,Tm ), Ti' = E(Ti), i = 1,...,m, где m [] n;
• возможность получить для произвольного выбранного злоумышленником открытого сообщения T соответствующий шифротекст T' = E(T);
• возможность получить для произвольного выбранного злоумышленником шифрованного сообщения T' соответствующий открытый текст T = D(T');

Соответственно этим трем возможностям различают следующие основные виды криптоанализа:

• анализ на основе только шифротекста;
• анализ на основе невыбранного открытого текста;
• анализ на основе выбранного открытого текста;
• анализ на основе выбранного шифротекста;

Первая возможность есть в распоряжении аналитика практически всегда. Вторая возможность также вполне реальна: например, разведке через агентуру удалось достать расшифровку одного из секретных сообщений. Более того, эта возможность весьма типична в тех сферах, где срок жизни секретной информации весьма мал, и она быстро предается огласке – при передаче рекламных материалов, различных репортажей, публикуемых впоследствии средствами массовой информации и т.д., словом везде, где надо опередить конкурентов всего на несколько часов или дней. Третья и четвертая возможности, хотя и кажутся экзотическими, тем не менее также могут иметь место – если сотрудник организации, работающий на другую сторону, имеет доступ к общим шифровальным средствам. Конечно, третий случай имеет смысл применительно к задаче дешифрования, а четвертый – навязывания ложных данных. Первые два актуальны для обеих угроз.

В рассматриваемой нами жизненной ситуации присутствует еще одна сторона, роль которой попытаемся выполнить мы сами. Это криптограф, в задачу которого входит снабдить законных участников обмена такими алгоритмами за- и расшифрования, чтобы злоумышленник не смог выполнить ни одну из своих угроз даже в самой благоприятной для него ситуации, то есть при возможности криптоанализа на основе произвольно выбранного открытого текста. Иными словами, задачей криптографа является разработка секретной и аутентичной системы передачи данных. Вообще говоря, это различные, хотя порой и связанные довольно тесно в конкретных шифрах свойства криптосистем. Поясним их смысл:

Аутентичность есть защищенность криптографической системы от навязывания ложных данных.

Секретность есть защищенность криптографической системы от несанкциониро¬ванного ознакомления с содержимым закрываемых системой данных.

3. Шифры с секретным ключом.

Итак, наша задача заключается в том, чтобы снабдить участников обмена надежными алгоритмами шифрования. Первый вопрос, который мы себе зададим – это решаема ли задача в принципе, и если да, то какую максимальную степень секретности мы можем обеспечить? Ответ на этот вопрос был найден Шенноном – теорема, носящая его имя, гласит, что существуют абсолютно стойкие шифры, то есть такие шифры, которые невозможно раскрыть, даже если криптоаналитик обладает неограниченным запасом времени и вычислительных ресурсов. Шенноном также было установлено, что условием абсолютной стойкости шифра является использование в алгоритме шифрования не меньшего количества секретной информации, чем содержится информации в шифруемом сообщении.

Как реализовать такой шифр? Прежде чем отвечать на этот вопрос вспомним, что все современные шифры базируются на принципе Кирхгофа, который гласит, что алгоритмы шифрования должны строиться таким образом, чтобы даже при их разглашении они все еще обеспечивали определенный уровень надежности. Кстати, об авторе принципа – в литературе его ошибочно величают “Керкхоффом” – автор не встретил ни единого случая правильной транскрипции этой фамилии. Пишется она “Kirchhoff” – точно так же, как фамилия автора известных в электротехнике законов Кирхгофа. Кирхгоф был голландцем, а не англичанином, поэтому произносить его фамилию следует в соответствии с правилами немецкой транскрипции, а не английской. Вернемся к обсуждаемой теме – ясно, что криптоалгоритмы, построенные в соответствии с принципом Кирхгофа должны использовать при шифровании секретные данные, называемые ключом, которые и обеспечивают секретность сообщения в условиях открытости самого алгоритма. Другими словами, секретность шифра должна обеспечиваться

секретностью ключа, а не секретностью алгоритма шифрования. Это означает, что алгоритмы E и D, введенные нами в рассмотрение в предыдущем разделе, используют секретный ключ K, и могут быть обозначены нами теперь как EK и DK. Тогда уравнения шифрования будут иметь следующий вид:

T' = EK(T) (зашифрование),
T = DK(T') (расшифрование).

Вспомним, что в шифрах рассматриваемого класса для за- и расшифрования используется один и тот же ключ. Ясно, что процедура расшифрования должна в любом случае приводить к правильному результату. Это означает, что каковы бы ни были допустимые блок данных T и ключ K, должно выполняться следующее равенство: EK(DK(T)) = T.

Вернемся к абсолютно стойким шифрам, реализующим принцип Кирхгофа. Так как вся их секретность сосредоточена в ключе K, применительно к ним требование Шеннона означает, что размер ключа шифрования не должен быть меньше размера шифруемого сообщения: | K | [] | T |. Будем полагать, что они имеют одинаковый размер, равный N бит: | K | = | T | = N. Это минимум, при котором все еще возможна абсолютная стойкость. Для зашифрования сообщение T необходимо скомбинировать с ключом K с помощью некоторой бинарной операции ° таким образом, чтобы полученный шифротекст зависел и от исходного текста T, и от ключа K. При этом уравнение зашифрования будет иметь следующий вид:

T' = EK(T) = T ° K.

Размер шифротекста при этом также равен N бит: | T' | = | T | = | K | = N. Для обеспечения абсолютной стойкости шифра количество секретной информации в ключе K должно быть максимально возможным для его размера. Это означает, что все биты ключа должны быть случайны с равновероятными значениями и статистически независимы. Такой ключ может быть получен только аппаратным способом, алгоритмически его выработать нельзя, так как в этом случае указанное требование будет нарушено и шифр перестанет быть абсолютно стойким.

Обсудим теперь требования, которым должна удовлетворять операция °. Во-первых, чтобы шифрование было обратимым, уравнение T ° K = T' должно быть однозначно разрешимо относительно T при любых значениях T' и K. Это означает, что у бинарной операции ° должна существовать обратная, которую мы обозначим через •, и каковы бы ни были N-битовые блоки данных T и K, всегда должно выполняться равенство (T ° K) • K = T. Во вторых, для обеспечения полной секретности шифра необходимо, чтобы разные ключи давали для одинаковых исходных текстов разные шифротексты. Это равносильно требованию однозначной разрешимости уравнения T ° K = T' относительно K. Так как секретность шифрованного сообщения целиком опирается на секретность ключа, во всем остальном операции ° и • могут выбираться из соображений удобства. В качестве таких операций может использоваться сложение и вычитание по модулю 2N:

T ° K = (T + K) mod 2N, T • K = (T – K) mod 2N.

Осуществить вычисления над сообщением как единым целым может оказаться затруднительным по причине его значительного размера, поэтому целесообразно разбить сообщение и ключ на блоки меньшего размера и применить указанные операции к этим блокам:

T = (T1,T2,...,Tn), K = (K1,K2,...,Kn), |Ki| = |Ti| = Ni,
Ti ° Ki = (Ti + Ki) mod 2Ni, Ti • Ki = (Ti – Ki) mod 2Ni.

Если довести этот процесс дробления до логического конца, мы придем к операции побитового сложения по модулю 2, называемой также побитовым исключающим или:

T ° K = T • K = T [] K.

Последняя операция оказалась обратной к самой себе и по этой причине, а также в силу своей простоты и легкости реализации (отдельные биты сообщения в ней обрабатываются независимо друг от друга), получила наибольшее распространение.

Кратко остановимся на достигнутом: шифр, который мы сейчас получили, называется одноразовой гаммой Вернама. Этот шифр обладает абсолютной стойкостью, которая, однако, оплачивается достаточно дорогой ценой – для шифрования сообщения нужен ключ такого же размера, предварительно доставленный отправителю и получателю.

Для шифрования двух различных сообщений нельзя применять одну и ту же последовательность элементов гаммы. Если это требование нарушено, всегда можно найти такую пару бинарных операций [] и [], которые, будучи примененными соответственно к блокам открытых и зашифрованных с использованием одного и того же элемента гаммы данных, дадут идентичные результаты:

Как видим, результат совпадает с побитовой суммой по модулю 2 блоков открытого текста, что делает криптоанализ тривиальным.

Требование уникальной гаммы для каждого шифруемого сообщения делает шифрование с помощью одноразовой гаммы Вернама настолько накладным, что его использование экономически оправдано лишь в каналах связи для передачи сообщений исключительной важности, задействованных к тому же не слишком часто.

Барьер, перед которым мы остановились, непреодолим: достичь эффектив¬ности практической реализации криптоалгоритма можно только отказавшись от абсолютной стойкости. Шифр, не являющийся абсолютно стойким, можно раскрыть за конечное время, точнее, за конечное число шагов, каждый из которых состоит в выполнении элементарной арифметической или логической операции. Однако ничто не мешает нам создать такой теоретически нестойкий шифр, для раскрытия которого требовалось бы выполнить настолько большое число операций, чтобы это было неосуществимо на современных и ожидаемых в не очень далекой перспективе вычислительных средствах за разумное время. Мерой практической стойкости шифров подобного типа может служить количество работы, необходимое для их раскрытия, выраженное в элементарных операциях или в длительности соответствующих вычислений на современных компьютерах. Отметим, что в реальных системах криптозащиты информации используются почти исключительно теоретически нестойкие шифры.

Хороший шифр должен быть устойчив к статистическому и алгоритмическому анализу, то есть не должно существовать легко обнаружимых статистических связей между открытым и шифрованным текстом и зависимости между ними должны быть достаточно сложными для того, что бы их можно было обнаружить путем анализа. Есть четкая граница между хорошо и не очень хорошо спроектированными блочными шифрами: первый невозможно раскрыть способом, более эффективным чем полный перебор по всем возможным значениям ключа, для раскрытия второго могут оказаться пригодными и более эффективные способы. Как же строить стойкие шифры? Наука об этом засекречена практически везде, где имеют дело с криптографией – публикуются лишь соображения, носящие самый общий характер и не содержащие никакой конкретики. Приобщиться к этим тайным знаниям можно, лишь работая в соответствующем подразделении соответствующей специальной службы. Ну а мы с вами попытаемся рассмотреть проблему исключительно с позиции здравого смысла. По большому счету, можно пред ложить лишь два фундаментальных подхода к построению шифра с секретным ключом:

Второй подход к построению шифров с секретным ключом не содержит в себе никаких намеков на возможные способы его реализации. В следующем разделе статьи мы попытаемся нащупать эти способы сами.

4. Базовая идея блочного шифра.

Ясно, что назначение функции f заключается в том, чтобы маскировать зависимость между блоком T0 и гаммой для шифрования блока T1, которая из него вырабатывается. Для этого функция f должна быть секретным элементом нашего шифра – мы пока закроем глаза на это нарушение принципа Кирхгофа. Отметим очень важный факт: наша схема работоспособна при любой функции f, после расшифрования мы всегда получим те же самые данные, которые были перед зашифрованием.

Прежде чем перейти к изучению дальнейшего материала, читателям, не очень сильным в математике, стоит познакомиться с некоторыми математическими понятиями, а именно, с понятием композиции отображений и преобразований. Те же, кто владеет этим материалом в достаточной степени, могут не читать следующие абзацы, напечатанные мелким шрифтом.

Все рассматриваемые в данной части статьи преобразования являются операторами в множестве блоков данных, то есть функциями, принимающими в качестве аргумента и выдающими в качестве результата блоки данных.

1. Назовем композицией преобразований A и B такое преобразование C = AB, что каков бы ни был блок данных T, всегда выполняется равенство C(T) = B(A(T)). Таким образом, по определению композиции AB(T) = B(A(T)).

2. Для композиции преобразований справедлив ассоциативный закон, то есть для любых преобразований A, B, C справедливо тождество: A(BC) = (AB)C. Действительно, каким бы ни был блок данных T, справедливо следующее равенство:

(A(BC))(T) = BC(A(T)) = C(B(A(T))) = C(AB(T)) = ((AB)C)(T).

Поэтому в выражении для композиции трех и более преобразований скобки излишни: A(BC) = (AB)C = ABC.

3. Среди всех преобразований существует одно особое, называемое тождественным и обозначаемое нами через I. Отличительной особенностью данного преобразования является то, что оно оставляет свой аргумент неизменным: каков бы ни был блок данных T , всегда справедливо I(T) = T. Очевидно, что композиция любого преобразования A с тождественным дает в результате это же преобразование A: IA = AI = A. Действительно, для любого блока данных T справедливы следующие равенства: AI(T) = I(A(T)) = A(T) и IA(T) = A(I(T)) = A(T).

4. Преобразование B называется обратным к преобразованию A, если их композиция является тождественным преобразованием, то есть если выполняется условие AB = I или для произвольного блока данных T справедливо равенство B(A(T)) = T. Преобразование A называется обратимым, если существует обратное к нему преобразование, обозначаемое A^–1: AA ^-1 = I.

Теперь вспомним про то, что предложенная нами схема решила лишь половину проблемы, так как младшая часть T0 блока T осталась незашифрованной. Но эта проблема имеет очевидное решение: на следующем шаге необходимо зашифровать часть T0 массива T, используя элемент гаммы, выработанный из части T1' блока T с использованием некоторой другой функции g, отображающей N0-битовые блоки данных на N1-битовые. Теперь обе части исходного блока окажутся зашифрованными. По ряду причин, однако, принято, что шифруемая на каждом таком шаге и используемая для выработки гаммы части находятся на фиксированных позициях внутри блока – традиция предписывает вырабатывать гамму из младшей части и накладывать ее на старшую. По крайней мере, дело обстоит именно так в ГОСТе, DESе, и всех других шифрах, построенных по их образу и подобию. Для того, чтобы обеспечить указанное свойство, между шагами шифрования необходимо выполнить перестановку частей блока, помещающую соответствующие части на надлежащие места.

По соображениям обеспечения максимальной криптостойкости и эффективности реализации шифра целесообразно взять размеры старшей и младшей частей шифруемого блока одинаковыми: N0 = N1 = N/2. Именно такое условие выбрали разработчики большинства шифров рассматриваемой архитектуры. В этом случае между шагами алгоритма части шифруемого блока просто меняются местами. Однако существуют шифры, не подчиняющиеся этому правилу, о них будет сказано несколько слов ниже в настоящей статье.

Обозначим через S операцию перестановки старшей и младшей частей массива информации: S(T) = S(T0,T1) = (T1,T0). Очевидно, что операция S является обратной для самой себя: S2 = S • S = I. Действительно, для произвольного блока данных T = (T0,T1) справедливо равенство:

S2(T) = S2(T0,T1) = S(S(T0,T1)) = S(T1,T0) = (T0,T1) = T.

Тогда наша новая схема шифрования может быть представлена композицией более простых шагов:

Поскольку за один шаг алгоритма шифруется N1 < N/2 битов блока, то для зашифрования всего блока потребуется более двух шагов. Точное значение числа минимально требуемых шагов в таком алгоритме равно []N/N1[], где через []x[] обозначен результат округления числа x до ближайшего целого в сторону увеличения. Из соображения простоты реализации шифра обычно выбирают N1 так, чтобы размер блока N делился на него без остатка. Как правило, если N = 64, то берут N1 = 16 или N1 = 8.

Следует отметить, что шифров, построенных по такому принципу, намного меньше чем шифров, в которых блок делится на две одинаковые по размеру части. Обусловлено это тем, что в них за один шаг шифруется меньшее количество битов, и, соответственно, требуется больше шагов. По такому принципу, например, построен шифр под кодовым названием “албер”, созданный в недрах одного из многочисленных НИИ, и, поговаривают, даже претендовавший на место Российского стандарта шифрования, для него N1 = 8.

5. Шифр простой замены.

Для того, чтобы блочная схема шифрования была устойчива к криптоанализу, она должна обладать свойствами перемешивания и рассеивания. Это означает, что каждый бит исходного текста должен влиять на все биты шифротекста, причем характер этого влияния не должен быть прослеживаем ни статистически, ни алгоритмически. Это требование важно именно для блочных шифров по следующей причине: для раскрытия шифра по алгоритмической линии криптоаналитик может попытаться в явном виде вывести соотношения, связывающие входы и выходы алгоритма. Для потокового шифра это бесполезно, потому что эти соотношения целиком определяются элементами гаммы, которые различны для различных блоков шифруемых данных. А вот чтобы криптоанализ не увенчался успехом для блочного шифра, требуется, чтобы характер влияния входных данных на выходные был достаточно сложным для того, чтобы его можно было выявить путем анализа массивов входных и выходных данных. Это, в частности, подразумевает отсутствие статистической зависимости битов выходного блока от битов входного, что означает на практике, что каким бы образом мы ни изменили блок открытых данных T, все биты блока шифрованных данных T' = EK(T) с вероятностью 1/2 независимо друг от друга изменят свое значение. Но построенная в предыдущем разделе схема шифрования не обладает таким свойством. Действительно, пусть зашифрованию подвергается блок данных T = (T0,T1), тогда в результате мы получим:

Нам осталось обсудить последнюю деталь в построении блочного шифра. До сих пор мы не требовали, чтобы размер шифруемого блока T был постоянным, однако теперь нам придется это сделать по следующим причинам:

• Многие элементы шифра, такие, как перестановки битов и функции замены битовых групп в массиве данных предполагают, что преобразуемый блок имеет фиксированный размер. Хотя в принципе можно задавать правило построения таких элементов для блоков произвольного размера, применять это правило на практике было бы чрезвычайно неудобно.
• Если бы было возможно произвольно увеличивать размер шифруемого блока, это привело бы к ситуации, когда блок данных большого размера шифруется за один проход на ключе гораздо меньшего размера, и такая схема становится менее устойчивой к попыткам алгоритмического криптоанализа.

В силу указанных причин шифрованию по рассмотренной нами схеме должны подвергаться только блоки данных фиксированного размера, именно поэтому данный шифр называется блочным. При необходимости сообщение T разбивается на несколько блоков одинакового размера, которые шифруются независимо друг от друга:

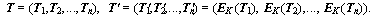По этой причине данную схему шифрования называют шифром простой замены, так как в конечном итоге она сводится к замене одних значений блоков данных на другие. Для построенного нами алгоритма шифрования, очевидно, существует проблема, если размер шифруемого текста не кратен размеру блока криптоалгоритма. Этот, и ряд других вопросов будут обсуждены в следующем разделе.

Размер блоков шифрования определяется разработчиком шифра из условия достижения необходимой криптостойкости. Выбор недостаточного размера блоков сделает возможным криптоанализ на основе статистических закономерностей. С другой стороны, неоправданное увеличение размера блока сделает шифр громоздким и неудобным для применения, поэтому в данном вопросе необходимо искать компромисс. Практически во всех известных автору шифрах рассматриваемой архитектуры используется размер блока, равный 64 битам.

В заключение подведем некоторый итог наших изысканий: Для определения блочного шифра необходимо задать следующее:

Как было отмечено выше, данная схема может быть обобщена на случай разделения шифруемого блока данных T на два неодинаковых по размеру подблока. Кроме того, могут быть добавлены дополнительные преобразования данных в начале, конце, или на промежуточных этапах криптопреобразования, и также вместо функции побитового исключающего или можно использовать какую-либо другую для наложения гаммы на части шифруемого блока. Шифр, который мы с вами только что построили, называется шифром простой замены, так как по сути его действие заключается в том, что шифруемые блоки данных заменяются на блоки шифротекста независимо от других блоков.

6. Российский стандарт шифрования.

Настало время рассказать об алгоритме шифрования, являющемся Российским стандартом. Этот стандарт имеет обозначение ГОСТ 28147-89 из которого явствует, что он был принят в 1989 году. Его основу составляют процедуры зашифрования и расшифрования по алгоритму простой замены 64-битовых блоков данных, и уже с их использованием строятся другие алгоритмы шифрования – как это сделать, обсуждается в следующих разделах. В настоящей статье рассматривается только криптоалгоритм ГОСТ 28147-89 [6], описание некоторых других шифров с подобной архитектурой можно найти в литературе [2,7,8], поэтому автор решил не останавливаться на них. Сейчас мы рассмотрим ГОСТ по намеченной выше схеме:

[] Иными словами, в ходе цикла зашифрования элементы ключа используются последовательно друг за другом, при этом ключ “просматривается” четыре раза – первые три в прямом направлении, четвертый – в обратном. Читатели, хорошо усвоившие материал предыдущих разделов, без труда сообразят, что в цикле расшифрования элементы ключа используются в обратном по отношению к циклу зашифрования порядке, то есть сначала ключ просматривается один раз в прямом направлении, затем три раза в обратном.

Теперь поговорим о таблице замен. Она является некоторым аналогом S-блоков (S-boxes) американского стандарта, но, в отличие от последнего, во-первых, одна и та же на всех шагах цикла шифрования и во-вторых, не фиксирована и является секретным элементом шифра. Следует отметить, что алгоритм шифрования обратим при любом заполнении узлов замен, даже если они и не задают правильные подстановки в 16-элементном множестве, то есть содержат повторяющиеся элементы замены: hi,j = hi,k при некоторых i, j, k (j [] k). Однако такая замена ведет к потере информации о заменяемом значении, и, как следствие, к снижению криптостойкости шифра, поэтому возможность этого не предусматривается в ГОСТе.

Отметим, что основным секретным элементом российского шифра является ключ. Алгоритм должен оставаться криптостойким даже в случае раскрытия таблицы замен, что, однако, имеет место не при всех ее возможных значениях. Существование “слабых” таблиц замен, то есть таблиц, при использовании которых криптостойкость шифра существенно снижается, не вызывает сомнения – примером здесь может служить тривиальная таблица, при использовании которой всякое значение заменяется на него же самого. Однако в широких кругах специалистов–криптографов доподлинно неизвестно, как много есть подобных таблиц и существует ли критерий, позволяющий для конкретной таблицы однозначно определить, является ли она слабой или нет. Очевидно, что если такие критерии и существуют, они тщательно засекречены, никакие данные по этому вопросу, равно как и по вопросу качества ключей, не публиковались в открытой печати.

Однако дело с выбором ключевых данных обстоит не так уж плохо – с вероятностью, незначительно отличающейся от единицы, случайным образом выбранные ключевые данные не приведут к катастрофическому снижению криптостойкости шифра, и стоимость его раскрытия по-прежнему останется достаточно высокой и вряд ли окажется по зубам какой-либо коммерческой структуре, пусть даже и очень крупной. Ну а госслужбы при необходимости смогут получить всю интересующую их информацию и не прибегая к дешифрованию. По этой причине для обычного пользователя, стоимость защищаемой информации которого не превышает суммы порядка нескольких сотен тысяч долларов США, вполне достаточно будет хорошего статистического качества ключевой информации, заключающегося в следующем:

• ключ должен быть массивом из 256 независимых битов с равновероятными значениями;
• таблица замен должна быть набором из восьми независимых узлов, каждый из которых является случайной подстановкой в 16-элементном множестве;

В добавлении следует сделать следующее замечание: если функции, выражающие биты результата замены через биты исходного блока получаются достаточно простыми, это будет ослаблять шифр. Так, безобидный на первый взгляд узел замен Hi = (9, 8, 3, 10, 12, 13, 7, 14, 0, 1, 11, 2, 4, 5, 15, 6) на самом деле является слабым, так как оставляет второй и третий биты группы неизменными, что становится очевидным, если записать его в табличной форме с двоичными значениями аргумента и функции:

Кроме этого, таблица замен может содержать обходные пути других типов, позволяющие расшифровать сообщение более эффективным образом, чем полным перебором по возможным значениям ключа – но это уже тема не для журнальной статьи.