Автор: Сотник С.Л.

Понятие образа. Проблема обучения распознаванию образов. Геометрический и струк-турный подходы. Гипотеза компактности. Обучение и самообучение. Адаптация и обучение.

Методы обучения распознаванию образов - перцептроны, нейронные сети, метод потен-циальных функций, метод группового учета аргументов, метод предельных упрощений, коллек-тивы решающих правил.

Методы и алгоритмы анализа структуры многомерных данных - кластерный анализ, ие-рархическое группирование.

Понятие образа

Образ, класс — классификационная группировка в системе классификации, объеди-няющая (выделяющая) определенную группу объектов по некоторому признаку.

Образное восприятие мира — одно из загадочных свойств живого мозга, позволяющее разобраться в бесконечном потоке воспринимаемой информации и сохранять ориентацию в океане разрозненных данных о внешнем мире. Воспринимая внешний мир, мы всегда произво-дим классификацию воспринимаемых ощущений, т. е. разбиваем их на группы похожих, но не тождественных явлений. Например, несмотря на существенное различие, к одной группе отно-сятся все буквы А, написанные различными почерками, или все звуки, соответствующие одной и той же ноте, взятой в любой октаве и на любом инструменте, а оператор, управляющий техниче-ским объектом, на целое множество состояний объекта реагирует одной и той же реакцией. Ха-рактерно, что для составления понятия о группе восприятий определенного класса достаточно ознакомиться с незначительным количеством ее представителей. Ребенку можно показать всего один раз какую-либо букву, чтобы он смог найти эту букву в тексте, написанном различными шрифтами, или узнать ее, даже если она написана в умышленн о искаженном виде. Это свойство мозга позволяет сформулировать такое понятие, как образ.

Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. Примерами образов могут быть: река, море, жид-кость, музыка Чайковского, стихи Маяковского и т. д. В качестве образа можно рассматривать и некоторую совокупность состояний объекта управления, причем вся эта совокупность состояний характеризуется тем, что для достижения заданной цели требуется одинаковое воздействие на объект. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и незави-симо друг от друга классифицируют одни и те же объекты. Именно эта объективность образов позволяет людям всего мира понимать друг друга.

Способность восприятия внешнего мира в форме образов позволяет с определенной дос-товерностью узнавать бесконечное число объектов на основании ознакомления с конечным их числом, а объективный характер основного свойства образов позволяет моделировать процесс их распознавания. Будучи отражением объективной реальности, понятие образа столь же объек-тивно, как и сама реальность, а поэтому это понятие может быть само по себе объектом специ-ального исследования.

В литературе, посвященной проблеме обучения распознавания образов (ОРО), часто вместо понятия образа вводится понятие класса.

Проблема обучения распознаванию образов (ОРО)

Одним из самых интересных свойств человеческого мозга является способность отве-чать на бесконечное множество состояний внешней среды конечным числом реакций. Может быть, именно это свойство позволило человеку достигнуть высшей формы существования живой материи, выражающейся в способности к мышлению, т. е. активному отражению объективного мира в виде образов, понятий, суждений и т. д. Поэтому проблема ОРО возникла при изучении физиологических свойств мозга.

Рассмотрим пример задач из области ОРО.

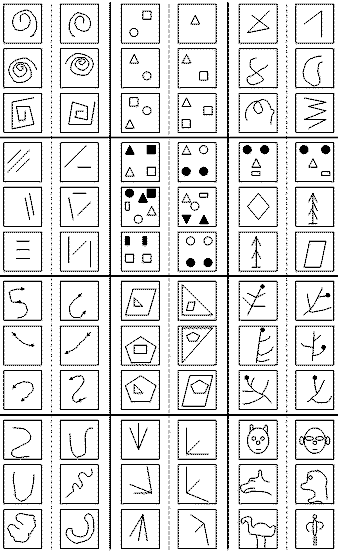Здесь представлены 12 задач, в которых следует отобрать признаки, при помощи кото-рых можно отличить левую триаду картинок от правой. Решение данных задач требует модели-рования логического мышления в полном объеме.

В целом проблема распознавания образов состоит из двух частей: обучения и распозна-вания. Обучение осуществляется путем показа отдельных объектов с указанием их принадлеж-ности тому или другому образу. В результате обучения распознающая система должна приобре-сти способность реагировать одинаковыми реакциями на все объекты одного образа и различ-ными — на все объекты различных образов. Очень важно, что процесс обучения должен завер-шиться только путем показов конечного числа объектов без каких-либо других подсказок. В ка-честве объектов обучения могут быть либо картинки, либо другие визуальные изображения (бу-квы), либо различные явления внешнего мира, например звуки, состояния организма при меди-цинском диагнозе, состояние технического объекта в системах управления и др. Важно, что в процессе обучения указываются только сами объекты и их принадлежность образу. За обучени-ем следует процесс распознавания новых объектов, который характеризует действия уже обу-ченной системы. Автоматизация этих процедур и составляет проблему обучения распознаванию образов. В том случае, когда человек сам разгадывает или придумывает, а затем навязывает машине правило классификации, проблема распознавания решается частично, так как основную и главную часть проблемы (обучение) человек берет на себя.

Проблема обучения распознаванию образов интересна как с прикладной, так и с прин-ципиальной точки зрения. С прикладной точки зрения решение этой проблемы важно прежде всего потому, что оно открывает возможность автоматизировать многие процессы, которые до сих пор связывали лишь с деятельностью живого мозга. Принципиальное значение проблемы тесно связано с вопросом, который все чаще возникает в связи с развитием идей кибернетики: что может и что принципиально не может делать машина? В какой мере возможности машины могут быть приближены к возможностям живого мозга? В частности, может ли машина развить в себе способность перенять у человека умение производить определенные действия в зависимо-сти от ситуаций, возникающих в окружающей среде? Пока стало ясно только то, что если чело-век может сначала сам осознать свое умение, а потом его описать, т. е. указать, почему он про-изводит действия в ответ на каждое состояние внешней среды или как (по какому правилу) он объединяет отдельные объекты в образы, то такое умение без принципиальных трудностей мо-жет быть передано машине. Если же человек обладает умением, но не может объяснить его, то остается только один путь передачи умения машине — обучение примерами.

Круг задач, которые могут решаться с помощью распознающих систем, чрезвычайно широк. Сюда относятся не только задачи распознавания зрительных и слуховых образов, но и задачи распознавания сложных процессов и явлений, возникающих, например, при выборе це-лесообразных действий руководителем предприятия или выборе оптимального управления технологическими, экономическими, транспортными или военными операциями. В каждой из таких задач анализируются некоторые явления, процессы, состояния внешнего мира, всюду далее называемые объектами наблюдения. Прежде чем начать анализ какого-либо объекта, нужно получить о нем определенную, каким-либо способом упорядоченную информацию. Такая информация представляет собой характеристику объектов, их отображение на множестве воспринимающих органов распознающей системы.

Но каждый объект наблюдения может воздействовать по-разному, в зависимости от ус-ловий восприятия. Например, какая-либо буква, даже одинаково написанная, может в принципе как угодно смещаться относительно воспринимающих органов. Кроме того, объекты одного и того же образа могут достаточно сильно отличаться друг от друга и, естественно, по-разному воздействовать на воспринимающие органы.

Каждое отображение какого-либо объекта на воспринимающие органы распознающей системы, независимо от его положения относительно этих органов, принято называть изображе-нием объекта, а множества таких изображений, объединенные какими-либо общими свойства-ми, представляют собой образы.

При решении задач управления методами распознавания образов вместо термина "изо-бражение" применяют термин "состояние". Состояние — это определенной формы отображение измеряемых текущих (или мгновенных) характеристик наблюдаемого объекта. Совокупность состояний определяет ситуацию. Понятие "ситуация" является аналогом понятия "образ". Но эта аналогия не полная, так как не всякий образ можно назвать ситуацией, хотя всякую ситуацию можно назвать образом.

Ситуацией принято называть некоторую совокупность состояний сложного объекта, ка-ждая из которых характеризуется одними и теми же или схожими характеристиками объекта. Например, если в качестве объекта наблюдения рассматривается некоторый объект управления, то ситуация объединяет такие состояния этого объекта, в которых следует применять одни и те же управляющие воздействия. Если объектом наблюдения является военная игра, то ситуация объединяет все состояния игры, которые требуют, например, мощного танкового удара при под-держке авиации.

Выбор исходного описания объектов является одной из центральных задач проблемы ОРО. При удачном выборе исходного описания (пространства признаков) задача распознавания может оказаться тривиальной и, наоборот, неудачно выбранное исходное описание может при-вести либо к очень сложной дальнейшей переработку информации, либо вообще к отсутствию решения. Например, если решается задача распознавания объектов, отличающихся по цвету, а в качестве исходного описания выбраны сигналы, получаемые от датчиков веса, то задача распо-знавания в принципе не может быть решена.

Геометрический и структурный подходы.

Каждый раз, когда сталкиваются с незнакомыми задачами, появляется естественное же-лание представить их в виде некоторой легко понимаемой модели, которая позволяла бы осмыс-лить задачу в таких терминах, которые легко воспроизводятся нашим воображением. А так как мы существуем в пространстве и во времени, наиболее понятной для нас является пространст-венно-временная интерпретация задач.

Любое изображение, которое возникает в результате наблюдения какого-либо объекта в процессе обучения или экзамена, можно представить в виде вектора, а значит и в виде точки некоторого пространства признаков. Если утверждается, что при показе изображений возможно однозначно отнести их к одному из двух (или нескольких) образов, то тем самым утверждается, что в некотором пространстве существует две (или несколько) области, не имеющие общих то-чек, и что изображения — точки из этих областей. Каждой такой области можно приписать на-именование, т. е. дать название, соответствующее образу.

Проинтерпретируем теперь в терминах геометрической картины процесс обучения рас-познаванию образов, ограничившись пока случаем распознавания только двух образов. Заранее считается известным лишь только то, что требуется разделить две области в некотором про-странстве и что показываются точки только из этих областей. Сами эти области заранее не оп-ределены, т. е. нет каких-либо сведений о расположении их границ или правил определения при-надлежности точки к той или иной области.

В ходе обучения предъявляются точки, случайно выбранные из этих областей, и сооб-щается информация о том, к какой области принадлежат предъявляемые точки. Никакой допол-нительной информации об этих областях, т. е. о расположении их границ, в ходе обучения не сообщается. Цель обучения состоит либо в построении поверхности, которая разделяла бы не только показанные в процессе обучения точки, но и все остальные точки, принадлежащие этим областям, либо в построении поверхностей, ограничивающих эти области так, чтобы в каждой из них находились только точки одного образа. Иначе говоря, цель обучения состоит в построе-нии таких функций от векторов-изображений, которые была бы, например, положительны на всех точках одного и отрицательны на всех точках другого образа. В связи с тем, что области не имеют общих точек, всегда существует целое множество таких разделяющих функций, а в ре-зультате обучения должна быть построена одна из них.

Если предъявляемые изображения принадлежат не двум, а большему числу образов, то задача состоит в построении по показанным в ходе обучения точкам поверхности, разделяющей все области, соответствующие этим образам, друг от друга. Задача эта может быть решена, на-пример, путем построения функции, принимающей над точками каждой из областей одинаковое значение, а над точками из разных областей значение этой функции должно быть различно.

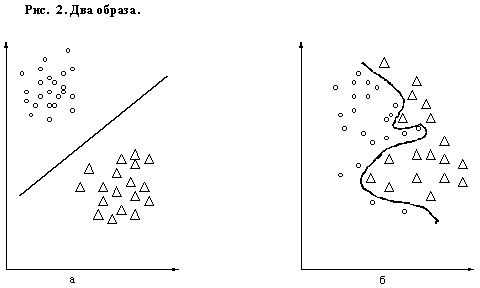На первый взгляд кажется, что знание всего лишь некоторого количества точек из об-ласти недостаточно, чтобы отделить всю область. Действительно, можно указать бесчисленное количество различных областей, которые содержат эти точки, и как бы ни была построена по ним поверхность, выделяющая область, всегда можно указать другую область, которая пересе-кает поверхность и вместе с тем содержит показанные точки. Однако известно, что задача о приближении функции по информации о ней в ограниченном множестве точек, существенно более узкой, чем все множество, на котором функция задана, является обычной математической задачей об аппроксимации функций. Разумеется, решение таких задач требует введения опреде-ленных ограничений на классе рассматриваемых функций, а выбор этих ограничений зависит от характера информации, которую может добавить учитель в процессе обучения. Одной из таких подсказок является гипотеза о компактности образов. Интуитивно ясно, что аппроксимация раз-деляющей функции будет задачей тем более легкой, чем более компактны и чем более разнесе-ны в пространстве области, подлежащие разделению. Так, например, в случае, показанном на Рис. 2а, разделение заведомо более просто, чем в случае, показанном на Рис. 2б. Действитель-но, в случае, изображенном на Рис. 2а, области могут быть разделены плоскостью, и даже при больших погрешностях в определении разделяющей функции она все же будет продолжать раз-делять области. В случае же на Рис. 2б, разделение осуществляется замысловатой поверхностью и даже незначительные отклонения в ее форме приводят к ошибкам разделения. Именно это ин-туитивное представление о сравнительно легко разделимых областях привело к гипотезе ком-пактности.

Наряду с геометрической интерпретацией проблемы обучения распознаванию образов существует и иной подход, который назван структурным, или лингвистическим. Поясним лин-гвистический подход на примере распознавания зрительных изображений. Сначала выделяется набор исходных понятий — типичных фрагментов, встречающихся на изображениях, и характе-ристик взаимного расположения фрагментов — "слева", "снизу", "внутри" и т. д. Эти исходные понятия образуют словарь, позволяющий строить различные логические высказывания, иногда называемые предположениями. Задача состоит в том, чтобы из большого количества высказы-ваний, которые могли бы быть построены с использованием этих понятий, отобрать наиболее существенные для данного конкретного случая.

Далее, просматривая конечное и по возможности небольшое число объектов из каждого образа, нужно построить описание этих образов. Построенные описания должны быть столь полными, чтобы решить вопрос о том, к какому образу принадлежит данный объект. При реали-зации лингвистического подхода возникают две задачи: задача построения исходного словаря, т. е. набор типичных фрагментов, и задача построения правил описания из элементов заданного словаря.

В рамках лингвистической интерпретации проводится аналогия между структурой изо-бражений и синтаксисом языка. Стремление к этой аналогии было вызвано возможностью ис-пользовать аппарат математической лингвистики, т. е. методы по своей природе являются син-таксическими. Использование аппарата математической лингвистики для описания структуры изображений можно применять только после того, как произведена сегментация изображений на составные части, т. е. выработаны слова для описания типичных фрагментов и методы их поис-ка. После предварительной работы, обеспечивающей выделение слов, возникают собственно лингвистические задачи, состоящие из задач автоматического грамматического разбора описа-ний для распознавания изображений. При этом проявляется самостоятельная область исследо-ваний, которая требует не только знания основ математической лингвистики, но и овладения приемами, которые разработаны специально для лингвистической обработки изображений.

Гипотеза компактности

Если предположить, что в процессе обучения пространство признаков формируется ис-ходя из задуманной классификации, то тогда можно надеяться, что задание пространство при-знаков само по себе задает свойство, под действием которого образы в этом пространстве легко разделяются. Именно эти надежды по мере развития работ в области распознавания образов стимулировали появление гипотезы компактности, которая гласит: образам соответствуют ком-пактные множества в пространстве признаков. Под компактным множеством пока будем пони-мать некие "сгустки" точек в пространстве изображений, предполагая, что между этими сгуст-ками существуют разделяющие их разряжения.

Однако эту гипотезу не всегда удавалось подтвердить экспериментально, но, что самое главное, те задачи, в рамках которых гипотеза компактности хорошо выполнялась (Рис. 2а), все без исключения находили простое решение. И наоборот, те задачи, для которых гипотеза не подтверждалась (Рис. 2б), либо совсем не решались, либо решались с большим трудом с при-влечением дополнительных ухищрений. Этот факт заставил по меньшей мере усомниться в справедливости гипотезы компактности, так как для опровержения любой гипотезы достаточно одного отрицающего ее примера. Вместе с этим, выполнение гипотезы всюду там, где удавалось хорошо решить задачу обучения распознаванию образов, сохраняло к этой гипотезе интерес. Сама гипотеза компактности превратилась в признак возможности удовлетворительного реше-ния задач распознавания.

Формулировка гипотезы компактности подводит вплотную к понятию абстрактного об-раза. Если координаты пространства выбирать случайно, то и изображения в нем будут распре-делены случайно. Они будут в некоторых частях пространства располагаться более плотно, чем в других. Назовем некоторое случайно выбранное пространство абстрактным изображением. В этом абстрактном пространстве почти наверняка будут существовать компактные множества точек. Поэтому в соответствии с гипотезой компактности множества объектов, которым в абст-рактном пространстве соответствуют компактные множества точек, разумно назвать абстракт-ными образами данного пространства.

Обучение и самообучение. Адаптация и обучение

Все картинки, представленные на Рис. 1, характеризуют задачу обучения. В каждой из этих задач задается несколько примеров (обучающая последовательность) правильно решенных задач. Если бы удалось подметить некое всеобщее свойство, не зависящее ни от природы обра-зов, на от их изображений, а определяющее лишь их способность к разделимости, то наряду с обычной задачей обучения распознаванию, с использованием информации о принадлежности каждого объекта из обучающей последовательности тому или иному образу можно было бы по-ставить иную классификационную задачу — так называемую задачу обучения без учителя. За-дачу такого рода на описательном уровне можно сформулировать следующим образом: системе одновременно или последовательно предъявляются объекты без каких-либо указаний об их при-надлежности к образам. Входное устройство системы отображает множество объектов на мно-жество изображений и, используя некоторое заложенное в нее заранее свойство разделимости образов, производит самостоятельную классификацию этих объектов. После такого процесса самообучения система должна приобрести способность к распознаванию не только уже знако-мых объектов (объектов из обучающей последовательности), но и тех, которые ранее не предъ-являлись. Процессом самообучения некоторой системы называется такой процесс, в результате которого эта система без подсказки учителя приобретает способность к выработке одинаковых реакций на изображения объектов одного и того же образа и различных реакций на изображения различных образов. Роль учителя при этом состоит лишь в подсказке системе некоторого объек-тивного свойства, одинакового для всех образов и определяющего способность к разделению множества объектов на образы.

Оказывается, таким объективным свойством является свойство компактности образов. Взаимное расположение точек в выбранном пространстве уже содержит информацию о том, как следует разделить множество точек. Эта информация и определяет то свойство разделимости образов, которое оказывается достаточным для самообучения системы распознаванию образов.

Большинство известных алгоритмов самообучения способны выделять только абстракт-ные образы, т. е. компактные множества в заданных пространствах. Различие между ними со-стоит, по-видимому, в формализации понятия компактности. Однако это не снижает, а иногда и повышает ценность алгоритмов самообучения, так как часто сами образы заранее никем не оп-ределены, а задача состоит в том, чтобы определить, какие подмножества изображений в задан-ном пространстве представляют собой образы. Хорошим примером такой постановки задачи являются социологические исследования, когда по набору вопросов выделяются группы людей. В таком понимании задачи алгоритмы самообучения генерируют заранее не известную инфор-мацию о существовании в заданном пространстве образов, о которых ранее никто не имел ника-кого представления.

Кроме того, результат самообучения характеризует пригодность выбранного простран-ства для конкретной задачи обучения распознаванию. Если абстрактные образы, выделяемые в процессе самообучения, совпадают с реальными, то пространство выбрано удачно. Чем сильнее абстрактные образы отличаются от реальных, тем "неудобнее" выбранное пространство для кон-кретной задачи.

Обучением обычно называют процесс выработки в некоторой системе той или иной ре-акции на группы внешних идентичных сигналов путем многократного воздействия на систему внешней корректировки. Такую внешнюю корректировку в обучении принято называть "поощ-рениями" и "наказаниями". Механизм генерации этой корректировки практически полностью определяет алгоритм обучения. Самообучение отличается от обучения тем, что здесь дополни-тельная информация о верности реакции системе не сообщается.

Адаптация — это процесс изменения параметров и структуры системы, а возможно, и управляющих воздействий на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы.

Обучение — это процесс, в результате которого система постепенно приобретает спо-собность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация — это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.

Перцептроны

Пока о проблеме обучения распознаванию образов удавалось говорить в общих чертах, не выделяя конкретные методы или алгоритмы, не возникало и трудностей, появляющихся вся-ких раз, когда приходится в огромном множестве конкретных примеров, характеризующиеся общими подходами к решению проблемы ОРО. Коварство самой проблемы состоит в том, что на первый взгляд все методы и алгоритмы кажутся совершенно различными и, что самое непри-ятное, часто никакой из них не годится для решения той задачи, которую крайне необходимо срочно решить. И тогда появляется желание выдумать новый алгоритм, который, может быть, достигнет цели. Очевидно, именно это привело к возникновению огромного множества алгорит-мов, в котором не так-то легко разобраться.

Одним из методов решения задач обучения распознаванию образов основан на модели-ровании гипотетического механизма человеческого мозга. Структура модели заранее постулиру-ется. При таком подходе уровень биологических знаний или гипотез о биологических механиз-мах является исходной предпосылкой, на которой базируются модели этих механизмов. Приме-ром такого направления в теории и практике проблемы ОРО является класс устройств, называе-мых перцептронами. Нужно отметить, что перцептроны на заре своего возникновения рассмат-ривались только как эвристические модели механизма мозга. Впоследствии они стали основопо-лагающей схемой в построении кусочно-линейных моделей, обучающихся распознаванию обра-зов.

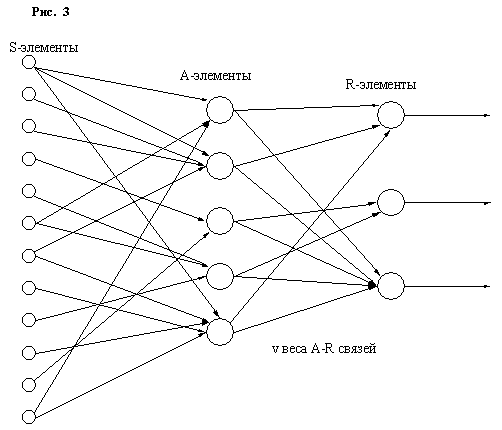В наиболее простом виде перцептрон (Рис. 3) состоит из совокупности чувствительных (сенсорных) элементов (S-элементов), на которые поступают входные сигналы. S-элементы слу-чайным образом связаны с совокупностью ассоциативных элементов (А-элементов), выход ко-торых отличается от нуля только тогда, когда возбуждено достаточно большое число S-элементов, воздействующих на один А-элемент. А-элементы соединены с реагирующими эле-ментами (R-элементами) связями, коэффициенты усиления (v) которых переменны и изменяют-ся в процессе обучения. Взвешенные комбинации выходов R-элементов составляют реакцию системы, которая указывает на принадлежность распознаваемого объекта определенному образу. Если распознаются только два образа, то в перцептроне устанавливается только один R-элемент, который обладает двумя реакциями — положительной и отрицательной. Если образов больше двух, то для каждого образа устанавливают свой R-элемент, а выход каждого такого элемента представляет линейную комбинацию выходов A-элементов:

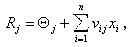где Rj — реакция j-го R-элемента; xi — реакция i-го A-элемента; vij — вес связи от i-го A-элемента к j-му R элементу; j — порог j-го R-элемента.

Аналогично записывается уравнение i-го A-элемента:

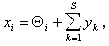Здесь сигнал yk может быть непрерывным, но чаще всего он принимает только два зна-чения: 0 или 1. Сигналы от S-элементов подаются на входы А-элементов с постоянными весами равными единице, но каждый А-элемент связан только с группой случайно выбранных S-элементов. Предположим, что требуется обучить перцептрон различать два образа V1 и V2. Бу-дем считать, что в перцептроне существует два R-элемента, один из которых предназначен обра-зу V1, а другой — образу V2. Перцептрон будет обучен правильно, если выход R1 превышает R2, когда распознаваемый объект принадлежит образу V1, и наоборот. Разделение объектов на два образа можно провести и с помощью только одного R-элемента. Тогда объекту образа V1 долж-на соответствовать положительная реакция R-элемента, а объектам образа V2 — отрицательная.

Перцептрон обучается путем предъявления обучающей последовательности изображе-ний объектов, принадлежащих образам V1 и V2. В процессе обучения изменяются веса vi А-элементов. В частности, если применяется система подкрепления с коррекцией ошибок, прежде всего учитывается правильность решения, принимаемого перцептроном. Если решение правиль-но, то веса связей всех сработавших А-элементов, ведущих к R-элементу, выдавшему правиль-ное решение, увеличиваются, а веса несработавших А-элементов остаются неизменными. Мож-но оставлять неизменными веса сработавших А-элементов, но уменьшать веса несработавших. В некоторых случаях веса сработавших связей увеличивают, а несработавших — уменьшают. После процесса обучения перцептрон сам, без учителя, начинает классифицировать новые объ-екты.

Если перцептрон действует по описанной схеме и в нем допускаются лишь связи, иду-щие от бинарных S-элементов к A-элементам и от A-элементов к единственному R-элементу, то такой перцептрон принято называть элементарным -перцептроном. Обычно классификация C(W) задается учителем. Перцептрон должен выработать в процессе обучения классификацию, задуманную учителем.

О перцептронах было сформулировано и доказано несколько основополагающих тео-рем, две из которых, определяющие основные свойства перцептрона, приведены ниже.

Теорема 1. Класс элементарных -перцептронов, для которых существует решение для любой задуманной классификации, не является пустым.

Эта теорема утверждает, что для любой классификации обучающей последовательности можно подобрать такой набор (из бесконечного набора) А-элементов, в котором будет осущест-влено задуманное разделение обучающей последовательности при помощи линейного решающе-го правила

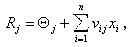Теорема 2. Если для некоторой классификации C(W) решение существует, то в процес-се обучения -перцептрона с коррекцией ошибок, начинающегося с произвольного исходного состояния, это решение будет достигнуто в течение конечного промежутка времени.

Смысл этой теоремы состоит в том, что если относительно задуманной классификации можно найти набор А-элементов, в котором существует решение, то в рамках этого набора оно будет достигнуто в конечный промежуток времени.

Обычно обсуждают свойства бесконечного перцептрона, т. е. перцептрона с бесконеч-ным числом А-элементов со всевозможными связями с S-элементами (полный набор A-элементов). В таких перцептронах решение всегда существует, а раз оно существует, то оно и достижимо в -перцептронах с коррекцией ошибок.

Очень интересную область исследований представляют собой многослойные перцептро-ны и перцептроны с перекрестными связями, но теория этих систем практически еще не разра-ботана.