
|
Поиск самой тяжелой общей подпоследовательности
Поиск самой тяжелой общей подпоследовательности, самой длинной возрастающей подпоследовательности, самой тяжелой возрастающей подпоследовательности
Частный случай задачи нахождения lis: Ниже описан алгоритм hcs Джекобсона и Во [Jacobson, Vo, 1992], выведенный из алгоритма поиска самой длинной возрастающей подпоследовательности (lis) Робинсона-Шенстеда [Schensted, 1961]. Представленые здесь алгоритмы модифицированы – в них исправлено построение направленных графов, используемых в процедурах. Прежде всего, вес общей для строк x и y подпоследовательности s можно определить следующим образом:
где (ip, jp) – пара сопоставленных символов из x и y, то есть Для вычисления hcs можно приспособить метод динамического программирования. Обозначим W(hcs(x(1, i), y(1, j))) как Wi,j. Тогда рекуррентное соотношение для Wi,j задается формулой
Соотношения следуют из метода вычисления матрицы l. В позиции (i, j), то есть когда рассматриваются префиксы x(1, i) и y(1, j), если xi = yj, новую общую подпоследовательность можно получить добавлением этого символа к текущей общей подпоследовательности строк x(1, i - 1) и y(1, j - 1), а ее вес – добавлением веса этого сопоставления к весу текущей общей подпоследовательности. В противном случае позиция (i, j) не меняет предыдущий результат. Таким образом, вес для позиции (i, j) задается самой тяжелой из предыдущих соседних позиций и, при определенных условиях, новым выведенным весом. Алгоритм Робинстона-Шенстера для вычисления lis строки y представлен на рисунке 21. L – это упорядоченный список пар (a, k), где a – символ строки, а k – его номер в строке. Каждая из следующих операций может быть выполнена за время O(log n), когда L реализуется с помощью сбалансированного дерева. insert(L, a) - вставить объект a в список L delete(L, a) - удалить объект из списка L next(L, a) - возвратить наименьший из строго больших a объектов в L prev(L, a) - возвратить наибольший из строго меньших a объектов в L max(L) - возвратить наибольший объект в L min(L) - возвратить наименьший объект в L Когда ничего не определено, процедуры Для каждого символа yj через a обозначим символ в L, после которого можно вставить yj, не нарушая строго возрастающий порядок в этом списке. Элемент, стоящий в L после a при этом заменяется на yj. Направленный граф символов строки создается с помощью массива node (узел). Элементами node являются указатели на узлы, созданные процедурой newnode, и содержащие символ, его номер в строке и адрес предыдущего узла. По завершении lis строки y можно воссоздать обратным перебором в графе - начиная с максимального компонента L.
- инициализация списка L
L = null
вычисление lis
for i = to n
(a, k) = prev(L, (yi, 0))
(b, l) = next(L, (a, k))
if b =/=null
delete(L, (b, l))
(L, (yi, i))
nodei = newnode((yi, i), nodek)
- инициализация списка L
L = null
- вычисление his
for i = 1 to n
(a, u, k) = prev(L, (yi, 0, 0))
(b, v, l) = next(L, (a, u, k))
while ((b, v, l) =/=null) and (u + f(i, yi) > v)
delete(L, (b, v, l))
(b, v, l) = next(L, (b, v, l))
if ((b, v, l) = null) or (yi < B)
INSERT(L, (Yi, u + f(i, yi), i))
nodei = newnode((yi, u + f(i, yi), i), nodek)
Обратите внимание, что and в цикле while является условным, т.е. второй операнд вычисляется, только в случае, если первый оказался истинным.
Для вычисления his необходимо, по мере работы процедуры, прослеживать кумулятивные общие веса his последовательно удлиняющихся префиксов строк. Компонентами L, таким образом, можно сделать тройки (a, u, k), где a – символ входной строки, u – общий вес his, заканчивающейся символом a, а k – номер a в строке. L остается строго монотонным по всем трем своим компонентам. Поэтому порядок в L можно поддерживать соответствующим алфавитному порядку первых элементов пары. Алгоритм вычисления his, основанный на алгоритме для lis, приведен на рисунке 22. Снова a обозначает наибольший из меньших yi символов в L, так что последний можно добавить к любой возрастающей подпоследовательности, заканчивающейся символом a, и опять получить возрастающую подпоследовательность. Если таких a нет, то u берется равным 0. Цикл while обеспечивает поддержание строгой монотонности второго элемента тройки. Затем новая тройка вставляется в список L, если это согласуется со строгим возрастанием первого элемента троек. Массив node применяется для построения связанной структуры для воссоздания фактической his по завершению процесса. Рассмотрим состояние списка L в конце каждой итерации, обозначаемое Li. Для каждой компоненты (a, u, k) из Li можно воссоздать возрастающую последовательность префикса y(1, i), заканчивающуюся a, путем обратного прохода от символа a в направленном графе. Далее будет показано, что для каждой возрастающей подпоследовательности s(1, k) префикса y(1, i) существует элемент b списка Li, такой, что b < sk, т.е. прерывающий возрастающую подпоследовательность в графе, не менее тяжелую, чем s(1, k). Таким образом, максимальный символ Li вместе с графом дают his префикса y(1, i). Следовательно, максимальный элемент L по завершении процесса определяет his для всей строки y. Приведенное выше утверждение очевидно правильно для i = 1. Предположим, что оно справедливо для итерации i - 1, и рассмотрим ситуацию для итерации i. Пусть s(1, k) – это возрастающая подпоследовательность для префикса y(1, i). Из вышеупомянутого, если sk = yi, то в Li-1 имеется элемент b < sk-1, определяющий возрастающую подпоследовательность, не менее тяжелую, чем s(1, k - 1). Итак, элемент b не может быть удален из списка на этой итерации, поскольку b < yi. В конце i-й итерации yi либо вставляется в список, либо уже там присутствует. Помня, что кумулятивные веса в L являются строго возрастающими, можно видеть, что возрастающая подпоследовательность, определяемая yi, удовлетворяет сделанному предположению. Теперь перейдем к ситуации, когда sk =/=yi. Здесь имеются две возможности: sk < yi и sk > yi. В первом случае предположение выполняется, так как часть списка, предшествующая yi, не затрагивается i-й итерацией. Остается рассмотреть случай, когда sk > yj. Последовательность s(1, k) тогда должна быть также возрастающей подпоследовательностью y(1, i-1). Таким образом, должна существовать возрастающая подпоследовательность, определяемая некоторым b в Li-1, не менее тяжелая, чем s(1, k). Если b имеется в Li, предположение очевидно выполняется. В противном случае b должен быть исключен из L на i-й итерации, причем взвешивающее условие цикла while гарантирует, что последовательность, определяемая yi, является не менее тяжелой, чем предыдущая, определяемая b. Таким образом, мы показали, что наше предположение справедливо при всех обстоятельствах, поэтому алгоритм корректно вычисляет his входной строки. Основной цикл алгоритма повторяется n раз, причем каждая из выполняемых в нем операций требует не больше O(log n) времени. Обратите внимание, что общее количество итераций внутреннего цикла while не превышает n, так как каждый из n элементов y может быть вставлен или удален из списка L не больше одного раза. Таким образом, временная сложность этого алгоритма составляет O(n log n).
i 1 2 3 4 5 6 7 8 9
Yi z e i t g e i s t
f(i,yi) 1 1 1 1 1 2 2 1 2
Li (z,1) (e,1) (e,1) (e,1) (e,1) (e,2) (e,2) (e,2) (e,2)
(i,2) (i,2) (g,2) (t,3) (i,4) (i,4) (i,4)
(t,3) (t,3) (s,5) (s,5)
(t,7)
Работу этого метода можно проиллюстрировать следующим примером. Выше приведены компоненты (a, u) троек списка L на каждом шаге i для случая y = zeitgeist. Заметим, что lis в этой строке является eigst. Однако, для первого появления символа в строке веса выбираются равными 1, а для второго – равными 2. При этих условиях возрастающая подпоследовательность eist, использующая вторые e и i, тяжелее, чем lis eigst. По завершении (t, 7), максимальный элемент L, используется для воссоздания пути e Направленный граф null <--- (z, 1) null <--- (e, 1) <--- (i, 2) <--- (t, 3) | –---<--- (g, 2) null <--- (e, 2) <--- (i, 4) <--- (s, 5) <--- (t, 7) Если сопоставления (i, j) между строками x и y записать в порядке возрастания i и в порядке убывания j для равных значений i, то каждая общая подпоследовательность очертит возрастающую подпоследовательность последовательности значений j. И наоборот, общую подпоследовательность можно вывести из возрастающей подпоследовательности значений j. Убывающий порядок j для одинаковых i предотвращает включение в подпоследовательность нескольких символов y, сопоставляемых одному символу x. Ниже приведен пример для строк preterit и zeitgeist. Подчеркнутые символы образуют lis последовательности j, соответствующую lcs этих двух строк.
i 1 2 3 4 5 6 7 8
xi p r e t e r i t
- - - - -
j 1 2 3 4 5 6 7 8 9
yj z e i t g e i s t
- - - - -
Сопоставления
i 3 3 4 4 5 5 7 7 8 8
j 6 2 9 4 6 2 7 3 9 4
- - - -
В приведенном выше упорядочении сопоставлений, соответствующие веса f(i, j, xi) можно приписать значениям j. Реализующий это метод, приведенный на рисунке 23, является обобщением алгоритма lcs Ханта-Шиманского. Обратите внимание, что для простоты здесь показаны только компоненты (a, u) троек списка L. Массив position содержит упорядоченный список позиций вхождения символов в y. Этим он похож на matchlist алгоритма Ханта-Шиманского. Последний давался в порядке убывания, в то время как списки массива positions даются в порядке возрастания. Правильный порядок сопоставлений достигается продвижением назад от позиции j до позиции
- построение упорядоченных списков позиций символов в y
for i = 1 to n
Обратите внимание, что and в цикле while является ‘условным’
Общая длина последовательностей значений j равна числу сопоставлений, r. Время счета зависит также от размера списка L, который ограничен длиной более короткой из двух входных строк. Таким образом, общее время выполнения составляет O((r + m)log n). Следующий пример иллюстрирует вычисление hcs. Как упоминалось в предыдущей главе, весовая функция минимального расстояния может применяться для указания предпочтений при выборе общих подпоследовательностей для близко выровненных сопоставлений. Рассмотрим пару строк warfare и forewarn. Ниже приведены общие подпоследовательности этой пары вместе с их весами согласно весовой функции минимального расстояния 8 - |i - j|, которая вознаграждает близко выровненные сопоставления. Веса всей lcs даются в скобках. i 1 2 3 4 5 6 7 xi w a r f a r e yj f o r e w a r n j 1 2 3 4 5 6 7 8 xi w a r w a r w a r i 1 2 3 1 2 6 1 5 6 j 5 6 7 5 6 7 5 6 7 8 - |i - j| 4 4 4 (12) 4 4 7 (15) 4 7 7 (18) xi r a r f a r f r e i 3 5 6 4 5 6 4 6 7 j 3 6 5 1 6 7 1 3 4 8 - |i - j| 8 7 7 (22) 5 7 7 (19) 5 5 5 (15) Мы видим, что самой тяжелой из lcs является rar. Состояние списка L после каждого этапа i вычисления hcs(warfare, forewarn) для данной взвешивающей функции показано ниже, вместе получившимся направленным графом. И снова для простоты даются только компоненты (a, u).
i 1 2 3 4 5 6 7
xi w a r f a r e
Li (5,4) (5,4) (3,8) (1,5) (1,5) (1,5) (1,5)
(6,8) (7,12) (3,8) (3,8) (3,10) (3,10)
(7,12) (6,15) (6,15) (4,15)
(7,22) (7,22)
Направленный граф null <--- (5, 4) <--- (6, 8) <--- (7, 12) NULL <--- (3, 8) <--- (6, 15) <--- (7, 22) NULL <--- (1, 5) <--- (3, 10) <--- (4, 15) По завершении максимальный элемент L, а именно, (7, 22) используется для получения пути 3 Частным случаем задачи hcs является случай, когда веса не зависят от позиции, то есть когда f является функцией только символов. Ниже обсуждается алгоритм, позволяющий воспользоваться даваемыми этим частным случаем преимуществами. Когда весовая функция не зависит от позиции, все веса, соответствующие позициям j в списке Если j уже присутствует в списке L, то b присваивается значение j. Если вход в L, непосредственно предшествующий j, тот же, что и при вставке j, то алгоритм просто удалит j из L, а затем заново вставит его в ту же точку. Таким образом, когда элемент j вставляется в L, он может быть удален из - построение упорядоченных списков позиций символов в y for i = 1 to nОбратите внимание, что and в цикле while является ‘условным’ И наконец, когда веса не зависят от позиции, условие вставки j в L можно не проверять. Значение b не может быть меньше j, так как a является наибольшим из меньших j элементов списка L. Таким образом, b > j. В случае, когда b > j, j можно вставить в L между a и b не нарушая монотонности списка. Если b = j, j можно смело вставлять вместо b, так как их веса одинаковы. Отсюда и видно, что j можно безбоязненно вставлять в L. На рисунке 24 приведен алгоритм hcs, включающий описанные выше усовершенствования для случая весов, не зависящих от позиции; в алгоритме опять для простоты опущено построение направленного графа и указаны только пары (a, u) триплетов списка L. Если веса всех символов алфавита равны, этот алгоритм превращается в алгоритм lcs Апосто-Гиерра. |
Автор проекта: USU Software
Вы можете выкупить этот проект.

 , а f – весовая функция.
, а f – весовая функция.
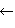 is
is для каждого i. К полученной последовательности значений j применяется алгоритм his. Соответствующую hcs(x, y) можно воссоздать после завершения процесса по направленному графу, построение которого в алгоритме также опущено для простоты.
для каждого i. К полученной последовательности значений j применяется алгоритм his. Соответствующую hcs(x, y) можно воссоздать после завершения процесса по направленному графу, построение которого в алгоритме также опущено для простоты. - инициализация списка L
L = null
- вычисление hcs
for i = 1 to n
- инициализация списка L
L = null
- вычисление hcs
for i = 1 to n
 while j =/=null
(a, u) = prev(L, (j, 0))
(b, v) = next(L, (a, u))
while ((b, v) =/=null) and (u + f(i, j, xi) > v)
delete(L, (b, v))
if ((b, v) = null) or (j < B)
INSERT(L, (J, U + F(I, J, Xi)))
while j =/=null
(a, u) = prev(L, (j, 0))
(b, v) = next(L, (a, u))
while ((b, v) =/=null) and (u + f(i, j, xi) > v)
delete(L, (b, v))
if ((b, v) = null) or (j < B)
INSERT(L, (J, U + F(I, J, Xi)))

 - инициализация списка L
L = null
- вычисление hcs
for i = 1 to m
- инициализация списка L
L = null
- вычисление hcs
for i = 1 to m
 insert(L, (j, u + f(xi)))
delete(
insert(L, (j, u + f(xi)))
delete(