Автор: Сотник С.Л.

Общая схема построения алгоритмов метода группового учета аргументов (МГУА).

Рис. 9. Селекция самого черного тюльпана при расширяющемся опытном поле (эквивалент полного перебора), и при постоянном размере поля (эквивалент селекции при сохранении свободы выбора решений F = const).

Заимствование алгоритмов переработки информации у природы является одной из ос-новных идей кибернетики. "Гипотеза селекции" утверждает, что алгоритм массовой селекции растений или животных является оптимальным алгоритмом переработки информации в слож-ных задачах. При массовой селекции высевается некоторое количество семян. В результате опы-ления образуются сложные наследственные комбинации. Селекционеры выбирают некоторую часть растений, у которых интересующее их свойство выражено больше всего (эвристический критерий). Семена этих растений собирают и снова высевают для образования новых, еще более сложных комбинаций. Через несколько поколений селекция останавливается и ее результат яв-ляется оптимальным. Если чрезмерно продолжать селекцию, то наступит «инцухт» — вырожде-ние растений. Существует оптимальное число поколений и оптимальное количество семян, от-бираемых в каждом из них.

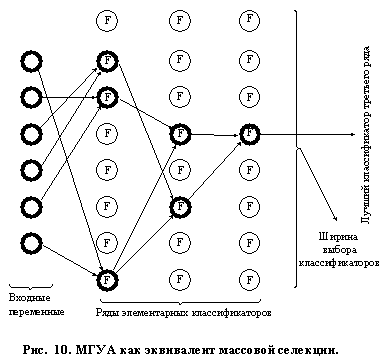
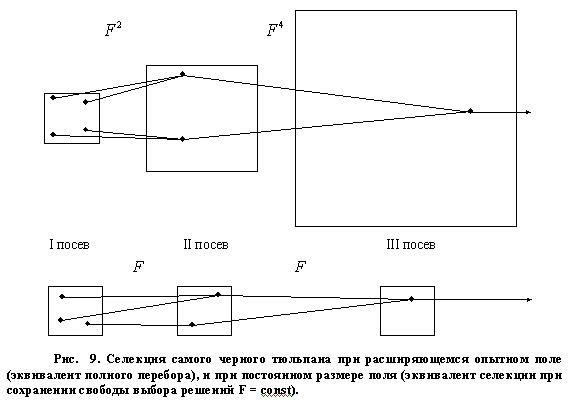Алгоритмы МГУА воспроизводят схему массовой селекции [5], показанной на Рис. 9. В них есть генераторы усложняющихся из ряда в ряд комбинаций и пороговые самоотборы луч-ших из них. Так называемое «полное» описание объекта

[] = f(x1,x2,x3,[],xm),

где f — некоторая элементарная функция, например степенной полином, заменяется нескольки-ми рядами "частных" описаний:

1-ряд селекции: y1= f(x1x2), y2= f(x1x3),..., ys= f(xm-1xm),

2-ряд селекции: z1= f(y1y2), z2= f(y1y2),..., zp= f(ys-1ys), где s=c2, p=cs2 и т.д.

Входные аргументы и промежуточные переменные сопрягаются попарно, и сложность комбинаций на каждом ряду обработки информации возрастает (как при массовой селекции), пока не будет получена единственная модель оптимальной сложности.

Каждое частное описание является функцией только двух аргументов. Поэтому его ко-эффициенты легко определить по данным обучающей последовательности при малом числе уз-лов интерполяции [4]. Исключая промежуточные переменные (если это удается), можно полу-чить "аналог" полного описания. Математика не запрещает обе эти операции. Например, по де-сяти узлам интерполяции можно получить в результате оценки коэффициентов полинома сотой степени и т. д.

Из ряда в ряд селекции пропускается только некоторое количество самых регулярных переменных. Степень регулярности оценивается по величине среднеквадратичной ошибки (средней для всех выбираемых в каждом поколении переменных или для одной самой точной переменой) на отдельной проверочной последовательности данных. Иногда в качестве показате-ля регулярности используется коэффициент корреляции.

Ряды селекции наращиваются до тех пор, пока регулярность повышается. Как только достигнут минимум ошибки, селекцию, во избежание "инцухта", следует остановить. Практиче-ски рекомендуется остановить селекцию даже несколько раньше достижения полного минимума, как только ошибка начинает падать слишком медленно. Это приводит к более простым и более достоверным уравнениям.

Алгоритм с ковариациями и с квадратичными описаниями.

В этом алгоритме [5, 6] используются частные описания, представленные в следующих формулах:

yi=a0+a1xi+a2xj+a3xixj;
yk=a0+a1xi+a2xj+a3xixj+a4xi2+a5xj2.

Сложность модели увеличивается от ряда к ряду селекции как по числу учитываемых аргументов, так и по степени. Степень полного описания быстро растет. На первом ряду — квадратичные описания, на втором — четвертой степени, на третьем — восьмой и т. д. В связи с этим минимум критерия селекции находится быстро, но не совсем точно. Кроме того, имеется опасность потери существенного аргумента, особенно на первых рядах селекции (в случае отсут-ствия протекции). Специальные теоремы теории МГУА определяют условия, при которых ре-зультат селекции не отличается от результата полного перебора моделей.

Для того чтобы степень полного уравнения повышалась с каждым рядом селекции на единицу, достаточно рассматривать все аргументы и их ковариации как обобщенные аргументы и пользоваться составленными для них линейными описаниями.

Метод предельных упрощений (МПУ)

По тому, как организован процесс обучения распознающих систем, четко выделяются два подхода к проблеме ОРО. Первый основан на построении сложных разделяющих поверхно-стей в случайно выбранных пространствах, а во втором — центр тяжести проблемы переносится на достижение понимания принципов формирования такого описания объектов, в рамках кото-рого сам процесс распознавания чрезвычайно прост. Обучение в этом случае рассматривается как некий процесс конструирования пространств для решения конкретных задач.

В МПУ предполагается, что разделяющая функция задается заранее в виде линейного (самого простого) полинома, а процесс обучения состоит в конструировании такого пространства минимальной размерности, в котором заранее заданная наиболее простая разделяющая функция безошибочно разделяет обучающую последовательность. МПР назван так потому, что в нем строится самое простое решающее правило в пространстве небольшой размерности, т. е. в про-стом пространстве.

Пусть на некотором множестве объектов V заданы два подмножества V*1 и V*2, опреде-ляющих собой образы на обучающей последовательности V. Рассмотрим i-е свойство объектов, такое, что некоторые объекты обучающей последовательности этим свойством обладают, а дру-гие — нет. Пусть заданным свойством обладают объекты, образующие подмножество V1i, а объ-екты подмножества V2i этим свойством не обладают (V1i [] V2i = V). Тогда i-е свойство называ-ют признаком первого типа относительно образа V*1, если выполняются соотношения

то это же свойство объявляется признаком второго типа относительно образа V*2. Если свойство не обладает ни одной из приведенных особенностей, то оно вообще не относится к при-знакам и не участвует в формировании пространства.

Одинаковые признаки — это два признака xi и xj, порождающие подмножества V1j, V2j, V1i, V2i, такие, что

V1j= V1i и V2j= V2i. (ф. 22)

Доказано утверждение, смысл которого заключается в том, что если пространство кон-струировать из однотипных, но неодинаковых признаков, то в конце концов будет построено такое пространство, в котором обучающая последовательность будет безошибочно разделена на два образа линейным, т. е. самым простым, решающим правилом.

Метод предельных упрощений состоит в том, что в процессе обучения последовательно проверяются всевозможные свойства объектов и из них выбираются только такие, которые об-ладают хотя бы одной из особенностей, определяемых соотношениями (ф. 18), (ф. 21). Такой отбор однотипных, но неодинаковых признаков продолжается до тех пор, пока при некотором значении размерности пространства не наступит безошибочное линейное разделение образов на обучающей последовательности. В зависимости от того, из признаков какого типа строится про-странство, в качестве разделяющей плоскости выбирается плоскость, описываемая уравнением

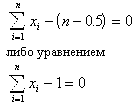Каждый объект относится к одному из образов в зависимости от того, по какую сторону относительно плоскости находится соответствующий этому объекту вектор в пространстве при-знаков размерности n.

Коллективы решающих правил

Давно известны приемы повышения качества принимаемых реше¬ний, состоящие в объ-единении специалистов той или иной области знаний в коллектив, вырабатывающий совместное решение. Идею коллективного решения можно применить и к «коллективу» фор¬мальных алго-ритмов, что позволит повысить эффективность ре¬шения многих задач.

Для рационального использования особенностей различных алгоритмов при решении задач распознавания возможно объединить различные по характеру алгоритмы распозна¬вания в коллективы, формирующие классификационное решение на основе правил, принятых в теории коллективных решений. Пусть в некоторой ситуации Х принимается решение S. Тогда S=R(X), где R—алгоритм принятия решения в ситуации X. Предположим, что существует L различных алгоритмов решения задачи, т. е. Sl=Rl(X), l=1, 2, ... , L, где Sl—решение, получен¬ное алгорит-мом Rl. Будем называть множество алгоритмов {R}={R1, R2, ..., Ri.} коллективом алгоритмов решения задачи (кол¬лективом решающих правил), если на множестве решений Sl в любой си-туации Х определено решающее правило F, т. е. S=F(S1, S2, ..., SL, X). Алгоритмы Rl принято называть членами коллектива, Sl — решением l-го члена коллектива, а S — коллек¬тивным ре-шением. Функция F определяет способ обобщения ин¬дивидуальных решений в решения коллек-тива S. Поэтому синтез функции F, или способ обобщения, является центральным момен¬том в организации коллектива.

Принятие коллективного решения может быть использовано при решении различных задач. Так, в задаче управления под си¬туацией понимается ситуация среды и целей управления, а под решением — самоуправление, приводящее объект в целевое состоя¬ние. В задачах прогноза Х — исходное, а S — прогнозируемое состояние. В задачах распознавания ситуацией Х является опи¬сание объекта X, т. е. его изображение, а решением S — номер образа, к которому принад-лежит наблюдаемое изображение. Индивидуальное и коллективное решения в задаче распозна¬вания состоят в отнесении некоторого изображения к одному из образов. Наиболее интересными коллективами распознающих ал¬горитмов являются такие, в которых существует зависимость веса каждого решающего правила Rl от распознаваемого изображения. Например, вес решающе-го правила Rl может определяется соотношением

для всех возможных значений X. Соотношение (ф. 25) означает, что решение коллекти-ва определяется решением того решающего правила Ri, области компетентности которого при-надлежит изоб¬ражение объекта X. Такой подход представляет собой двухуров¬невую процедуру распознавания. На первом уровне определяется принадлежность изображения той или иной об-ласти компетент¬ности, а уже на втором — вступает в силу решающее правило, компетентность которого максимальна в найденной области. Решение этого правила отождествляется с решени-ем всего кол¬лектива. Основным этапом в такой организации коллективного решения является обучение распознаванию областей компетентности. Прак¬тически постановкой этой задачи раз-личаются правила органи¬зации решения коллектива. Области компетентности можно ис¬кать, используя вероятностные свойства правил коллектива, можно применить гипотезу компактности и считать, что одина¬ковым правилам должны соответствовать компактные области, которые можно выделить алгоритмами самообучения. В про¬цессе обучения сначала выделяются ком-пактные множества и соответствующие им области, а затем в каждой из этих областей восста-навливается свое решающее правило. Решение такого пра¬вила, действующего в определенной области, объявляется дикта¬торским, т. е. отождествляется с решением всего коллектива.

В перцептроне каждый A-элемент может интерпретироваться как член коллектива. В процессе обучения все A-элементы при¬обретают веса, в соответствии с которыми эти A-элементы участ¬вуют в коллективном решении. Особенность каждого A-элемента состоит в том, что он действует в некотором подпространстве ис¬ходного пространства, характер которого опре-деляется связями между S- и A-элементами. Решение, получаемое на выходе перцептрона, мож-но интерпретировать как средневзвешенное реше¬ние коллектива, состоящего из всех A-элементов.