Автор: Сотник С.Л.

Представление в компьютере неформальных процедур. Языки логического программи-рования Рефал, Пролог, К-системы.

Элементы нечеткой логики.

Неформальные процедуры

Говоря о неформальных процедурах мы обычно хорошо понимаем, что имеется в виду, и без затруднений можем привести примеры таких процедур, связанных с пониманием текстов естественного языка, переводом с одного естественного языка на другой, информационным по-иском по смыслу и т. д.

Трудности возникают при попытке точного определения подобных процедур. Так, если рассматривать неформальные процедуры всего лишь как абстрактные функции, которые для каждого значения аргумента "выдают" некоторое значение, то категория неформальности вооб-ще исчезает из рассмотрения.

Неформальная процедура — это особый способ представления функций. Чтобы в какой-то степени приблизиться к этому "человеческому" способу представления функций, рассмотрим прежде всего традиционные алгоритмические модели и попытаемся понять, в чем состоит ос-новная трудность их применения для имитации неформальных процедур.

Алгоритмические модели

Алгоритмические модели основаны на понятии алгоритма. Исторически первые точные определения алгоритма, возникшие в 30-х годах, были связаны с понятием вычислимости. С тех пор было предложено множество, как выяснилось, эквивалентных определений алгоритма.

В практике программирования алгоритмы принято описывать с помощью алгоритмиче-ских языков программирования. Широко используются также разного рода блок-схемы алго-ритмов, позволяющие представить алгоритмы в наглядном и общедоступном виде, не привлекая в тоже время сложных конструкций из конкретных языков программирования.

Чтобы оценить возможности использования алгоритмов для представления неформаль-ных процедур, рассмотрим простую задачу.

ЗАДАЧА. Описать процедуру, реализующую преобразование из именительного падежа в родительный для существительных следующих типов: ДОМ, МАМА, ВИЛКА, КИНО, НОЧЬ, ТОКАРЬ, КИЛЬ.

Решение 1 указано на Рис. 13 в виде блок схемы соответствующего алгоритма.

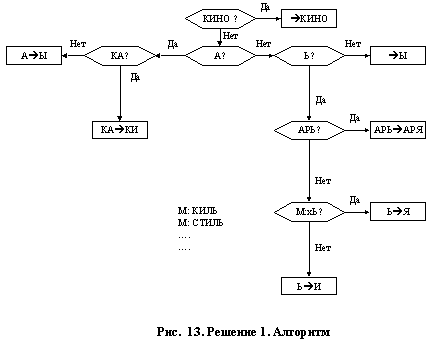С точки зрения программирования на алгоритмических языках достоинства подобного представления очевидны — эта блок-схема без затруднений переводится в текст программы, например, на языке Ассемблера или С++. Однако само составление подобной блок-схемы при появлении существительных новых типов становится, очевидно, все более и более утомитель-ным занятием. Для иллюстрации этого предположим, что дана

ДОПОЛНИТЕЛЬНАЯ ЗАДАЧА. Расширить алгоритм, представленный на Рис. 13 на слова ВАСЯ, ВРЕМЯ, АКЦИЯ, ЗАДАЧА.

Разумеется программист без особого труда составит соответствующую блок-схему алго-ритма. И все же, если учесть, что подобные изменения и расширения алгоритма при программи-ровании неформальных процедур происходят многократно (реальная сложность неформальной процедуры как раз и проявляется в практической невозможности предусмотреть заранее все слу-чаи), следует признать, что, вполне правильное в статике, решение 1 в динамике неудачно!

Продукционные модели

В подобных случаях для обеспечения динамичности процессов модификации программ используются те или иные варианты таблиц решений. С учетом этого для исходной задачи более приемлемо решение 2:

Таблица 1. Решение 2

Ситуация		Действие		Ситуация		Действие
--------		--------		--------		--------
КИНО		КИНО		-Ь		-И
-ча		-чи		-ие		-ия
-КА		-КИ		-мя		-мени
-А		-Ы		-я		-и
-АРЬ		-АРЯ		-		-А
-Ь & М:хЬ	-Я		

Соответствующая таблица решений содержит две графы — слева приведены описания ситуаций, справа — соответствующие действия. Предполагается, что программист разработал интерпретирующую программу для подобных таблиц. Эта программа работает следующим об-разом. Для конкретного входного слова, пусть это будет для примера слово РОЗА, осуществля-ется последовательный просмотр ситуаций, указанных в таблице, и сравнение их со входным словом. Если слово соответствует некоторой ситуации, то выполняется действие, указанное для этой ситуации.

Для слова РОЗА будет обнаружено соответствие с ситуацией "-А". В результате выпол-нения действия "-Ы" будет получено выходное слово РОЗЫ.

Теперь значительно упрощается расширение на новые классы слов — необходимо лишь обеспечить внесение вставок на нужное место в таблице решений.

Таблицы решений представляют собой частный случай так называемых продукционных систем. В этих системах правила вычислений представляются в виде продукций. Продукции представляют собой операторы специального вида и состоят из двух основных частей, для крат-кости называемых обычно "ситуация — действие".

"Ситуация" содержит описание ситуации, в которой применима продукция. Это описа-ние задается в виде условий, называемых посылками продукции. "Действие" — это набор инст-рукций, подлежащих выполнению в случае применимости продукции.

Режим возвратов

Таблица решений, приведенная на Таблица 1, иллюстрирует так называемую безвоз-вратную процедуру. В этом случае на каждом шаге выбирается единственное решение — так, для слова РОЗА таким решением будет РОЗЫ — проблема выбора решения не возникает. В об-щем случае неформальные процедуры являются многозначными, а правильность конкретного выбора, сделанного на некотором шаге, проверяется на следующих шагах. При этом использует-ся так называемый режим возвратов.

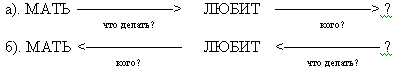Пусть предложение начинается со слов МАТЬ ЛЮБИТ ... . Проанализировав эти слова в первоначальном предположении именительного падежа для слова МАТЬ, система вправе по-строить структуру, представленную в случае а). Если следующее слово после слова ЛЮБИТ представляет собой существительное в винительном падеже, например, вся фраза имеет вид МАТЬ ЛЮБИТ СЫНА, то эта структура является окончательной. Если же фраза имеет вид МАТЬ ЛЮБИТ СЫН, то возникает противоречие или, как говорят, сигнал неуспеха — очеред-ное слово СЫН противоречит ожиданию прямого дополнения. В этом случае система должна вернуться на ближайший из предыдущих шагов, где можно принять другую альтернативу анали-за. В данном примере это шаг анализа слова МАТЬ — система должна принять теперь альтер-нативу винительного падежа для этого слова. Далее будет построена структура, указанная в слу-чае б).

Тривиальность рассмотренного примера убеждает в необходимости режима возвратов при реализации неформальных процедур.

Логический вывод

Важность логического вывода становится очевидной уже при рассмотрении простейших информационно-логических процедур. Предположим, что некоторая база данных содержит све-дения об отношениях "0 — ОТЕЦ у" и "х — МАТЬ у". Чтобы обработать запросы типа:

ИВАНОВ А.И. — ДЕД ПЕТРОВА В.А.?
ПЕТРОВ В.А. — ВНУК ИВАНОВА А.И.?

необходимо либо ввести в базу данных также и сведения об отношениях "х — ДЕД у" и "х — ВНУК у", либо объяснить системе, как из отношений ОТЕЦ, МАТЬ извлечь искомую ин-формацию. Реализация первой возможности связана с неограниченным ростом избыточности базы данных. Вторая возможность при традиционном алгоритмическом подходе требует напи-сания все новых и новых программ для реализации новых типов запросов.

Логический вывод позволяет расширять возможности "общения" наиболее просто и на-глядно. Так, для приведенных типов запросов системе достаточно будет сообщить три правила:

1. х—ДЕД у если х—ОТЕЦ а и а—РОДИТЕЛЬ у
2. х—РОДИТЕЛЬ у если х—ОТЕЦ у или х—МАТЬ у
3. х—ВНУК у если у—ДЕД х

Эти правила содержат естественные и очевидные определения понятий ДЕД, РОДИ-ТЕЛЬ, ВНУК. Поясним в чем состоит логический вывод для запроса "А—ДЕД В?" в предполо-жении, что в базе данных имеются факты: А—ОТЕЦ Б и Б—МАТЬ В. При этом для упрощения опустим тонкости, связанные с падежными окончаниями. Пользуясь определением 1 система придет к необходимости проверки существования такого индивидуума а, что факты А—ОТЕЦ а и а—РОДИТЕЛЬ В истинны. Если такой а существует, то А—ДЕД В, если не существует такого а, то А не является дедом В.

Зависимость продукций

Продукционные системы, содержащие аппарат логического вывода, отличает высокая степень общности правил обработки данных. Однако именно эта общность приводит к ухудше-нию динамических свойств соответствующих продукционных программ, к трудностям их моди-фикации и развития. Чтобы понять, в чем тут причина, обратимся снова к Таблица 1. Пока эта таблица содержит несколько строк, не представляет особого труда установление правильного порядка их следования, но если учесть, что реальное количество продукций в подобных задачах исчисляется сотнями и более, трудоемкость их правильного взаимного расположения становится очевидной. Практически, при программировании неформальных "человеческих" процедур, по-добные таблицы можно вручную создавать и сопровождать для нескольких десятков продукций, максимум — для 100-200 продукций. Продукции зависимы, и за правильное выявление этой зависимости отвечает программист. Новые продукции необходимо вручную вставлять на нужное место.

Мы могли бы использовать в таблице решений только конкретные факты, например правила ДОМ [] ДОМА, МАМА [] МАМЫ и т. д., и динамичность соответствующей таблицы решений была бы восстановлена — подобные правила можно было бы вводить в произвольном порядке! Однако цена подобной "динамичности" окажется непомерно высокой — полный отказ от обобщенных правил.

Желательно восстановить динамичность продукционно-логических систем, сохранив при этом в полном объеме возможность использования обобщенных правил. Продукционная система должна взять на себя функции распознавания и интерпретации приоритета продукций — программист должен только описывать ситуации и соответствующие им действия.

Продукционные системы с исключениями

Если отношение "правило—исключение" встроено в систему, она сама может понять, что преобразование ПАЛКА [] ПАЛКЫ незаконно. При этом система должна руководствовать-ся простым принципом: если применимо исключение, общее правило запрещено. Соответст-вующие системы будем называть системами с исключениями.

Отношение "общее правило — исключение" безусловно полезно для понимания систе-мой уместности правил. Можно сказать, что это отношение устанавливает автоматически (по умолчанию) наиболее типичное для неформальных процедур взаимодействие правил:

— исключение "вытесняет" общее правило.
— при пересечении разрешены оба правила.

Разумеется, возможны ситуации, когда необходимо поступать наоборот:

— исключение не запрещает общего правила
— при пересечении одно из правил запрещено.

Пусть дано, например, общее правило х [] р¬1 и его исключение Ах [] р2. Таким обра-зом, для произвольного слова необходима реакция р1. Для слова же, начинающегося с буквы А, исполняется реакция р2 — по умолчанию для таких слов реакция р1 незаконна.

Предположим, однако, что по условию конкретной задачи для слов, начинающихся с А, реакция р1 также допустима. В этом случае введение нового правила Ах [] р1 снимает запрет на реакцию р1 в ситуации Ах.

Аналогичный способ годится для пересечения правил.

Таким образом, аппарат исключений позволяет устанавливать произвольные способы взаимодействия правил, в том числе и отличные от взаимодействия по умолчанию.

При развитии продукционной системы с исключениями программист сосредотачивает свое внимание на выявлении новых правил и на обобщении уже имеющихся. Аппарат исключе-ний освобождает программиста от решения трудоемких вопросов согласования правил — распо-знавание и интерпретация исключений осуществляется автоматически.